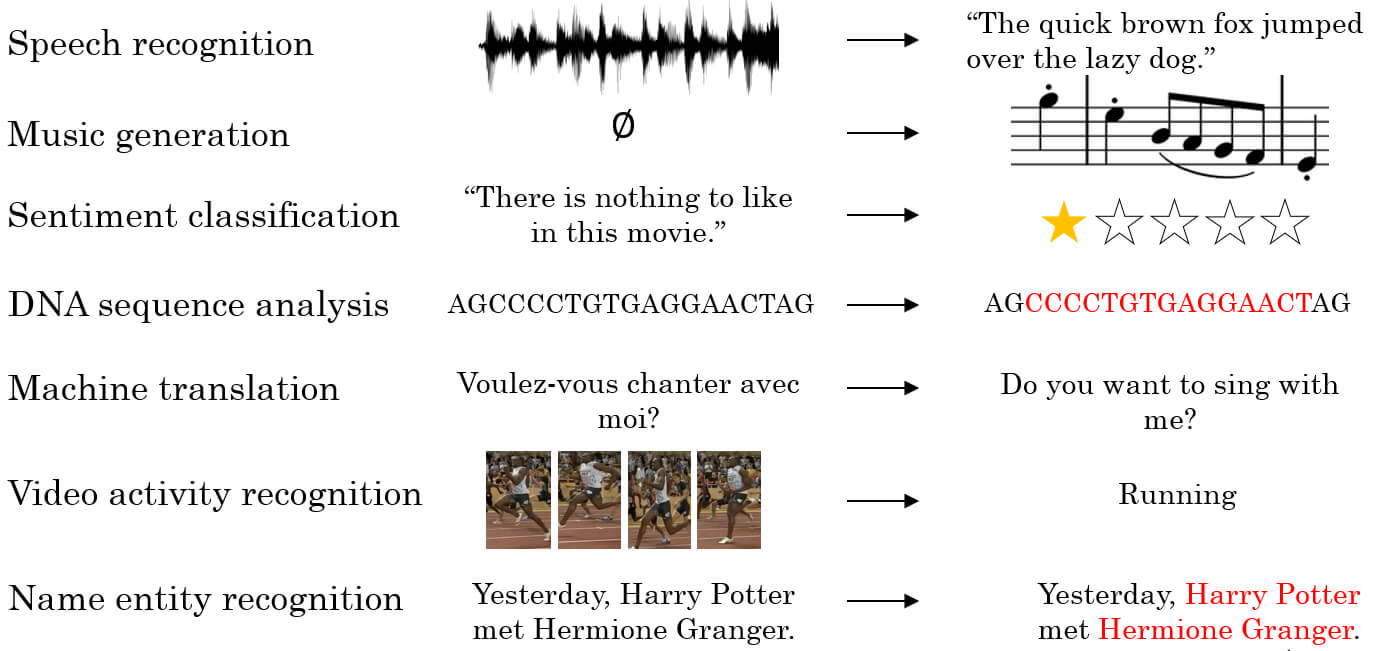
Sequence Models

Sequence data 指的是一連串的 data，例如輸入 input 一連串聲音 output 成文字（語音識別），我們要利用 Recurrent Neural Network (循環神經網路) 來建立出 sequence model。

Notation

假設有一個 name entity recognition 案例，要標示出所有的人名

\begin{aligned} x = \text{Harry Potter and Hermione Granger invented a new spell.}\\ y = \text{{\color{red}Harry Potter} and {\color{red}Hermione Granger} invented a new spell.} \end{aligned}

句子中每個字依照順序會標註成

\begin{aligned} \text{Harry} &: x^{<1>} \\ \text{Potter} &: x^{<2>} \\&... \end{aligned}

因為 y 跟 x 的字一模一樣，所以用 1 標示是要找的人名

\begin{aligned} \text{Harry}: y^{<1>} &= 1\\ \text{Potter}: y^{<2>} &= 1\\ \text{and}: y^{<3>} &= 0\\&... \end{aligned}

另外 $T_x = 9$ 表示句子的字數，同樣方式表達 y 的字數 $T_y = 9$ 。因為可能有多筆 training set，若要表示第 i 筆 data 的第 t 個字可以寫成 $X^{(i)<t>}, y^{(i)<t>}$ ；表達字數的方式也差不多： $T_x^{(i)} = 9, T_y^{(i)} = 9$ 。

Vocabulary (Dictionary)

通常我們會用一整個列表記錄所有單字，一個列表可能會有 30 ~ 100000 個單字

\begin{aligned} \begin{bmatrix} \text{a} \\ \text{aaron} \\\vdots \\\text{and}\\\vdots\\\text{Harry}\\\vdots\\\text{Potter}\\\vdots\\\text{zoo} \end{bmatrix} \end{aligned}

上面的案例是一個 10000 個單字的 dictionary
- and 的 index 在 367
- Harry 在 4075
- Potter 在 6830
接著用 one-hot 方式來呈現單字
- 例如 Harry 就會是一個全為 0 但 index=4075 為 1 的 10000 長度向量

\begin{aligned} x^{<1>} = \begin{bmatrix} 0\\0\\\vdots\\1 (4075^{th})\\\vdots\\0\\\vdots\\0 \end{bmatrix} \end{aligned}

該 model 的目標就是給定一堆 $x^{<t>}$ 找出各別對應的 $y^{<t>}$

Recurrent Neural Network Model

Why not standard network ?

以 Harry 例子來說，Input 9 個單字要產生 9 個 output，每個 input/output 又都是 10000 長的 one-hot vector
第一個問題
- 每個 training set 的 input 跟 output 會不斷改變
第二個問題
- Input features 之間並沒有 share 的關係
  - 在 $x^{<1>}$ 發現 Harry 是人名， $x^{<87>}$ 又是 Harry，那 1 能告訴 87 嗎?
第三個問題
- 參數太多，計算量太大
Recurrent Neural Network 沒有這些問題

RNNs

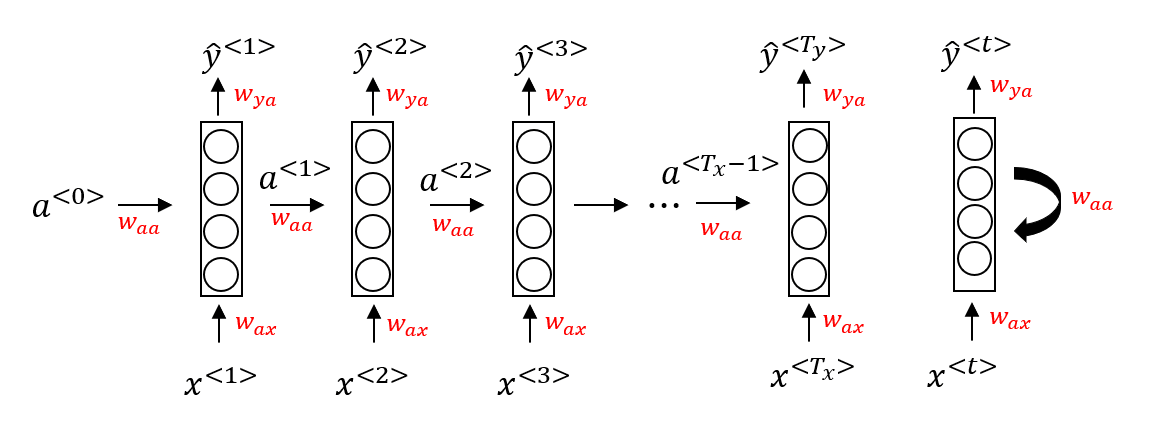
我們會先讀第一個單字 $x^{<1>}$
- 將他丟入 neural network 產生 $\hat{y}^{<1>}$
- 同時會產生 $a^{<1>}$ 給下一個單字 $x^{<2>}$ 使用
  - 通常 $a^{<0>}$ 是一個 0 vector
所以 $x^{<1>}$ 可以共享資訊給 $x^{<3>}$ 來產生 $\hat{y}_^{<3>}$
- 這個模型無法由 3 供應資訊給 1
- 之後會談到雙向的 RNNs (Bidirectional RNNs)
所有的 neural networks 會共享三大參數
- $W_{ax}, W_{aa}, W_{ya}$
- 命名的規則 (已 ax 為例) : 跟 x 作用並產生 a
以一般化 $x^{t}$ 來解釋每個單字在網路中的 forward propogation

\begin{aligned} a^{<0>} &= 0 \\ a^{<t>} &= \text{tanh}(W_{aa} a^{<t-1>} + W_{ax}x^{<t>} + b_a) \\ \hat{y}^{<t>} &= \text{softmax}(W_{ya}a^{<t>} + b_y) \end{aligned}

第一個 activation function 可選擇 tanh 或 ReLU
第二個 activation function 可選擇 sigmoid 或 softmax

Simplify Forward Propogation

為了講解之後較複雜的 RNNs，我們可以將 forward propogation 進一步簡化
將 Waa 和 Wax 合併為 Wa
- 若 Waa 是一個 100*100 矩陣
- 且 Wax 是一個 100*10000 矩陣
- 那麼 Wa 就是 100*10100 的寬矩陣

W_a = \begin{bmatrix} W_{aa} \mid W_{ax} \end{bmatrix}

將 $a^{<t-1>}$ 和 $x^{<t>}$ 也合併起來
- 若 a 是一個 100*1 向量
- 且 x 是一個 10000*1 向量
- 那麼合併後就是一個長為 10100*1 的向量

\begin{aligned} \begin{bmatrix} a^{<t-1>}\\ x^{<t>} \end{bmatrix} \end{aligned}

新的 forward propogation 公式

\begin{aligned} a^{<t>} &= \text{tanh}(W_a [a^{<t-1>};x^{<t>}] + b_a) \\ \hat{y}^{<t>} &= \text{softmax}(W_{y}a^{<t>}+ b_y) \end{aligned}

Backpropogation through time

RNNs 的 backpropogation 又稱作 backpropogation through time
- 因為由右至左推回來，像是時間逆流的感覺
要計算 backpropogation 之前，要先知道每個單字的 loss function
這邊使用 Cross-entropy loss 作為每個單字 (或說時間點) 的 loss function
也就是在 $x^{<t>}$ 時的 loss 表示為

\mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>}) = -y^{<t>}\log\hat{y}^{<t>} - (1-y^{<t>})\log(1-\hat{y}^{<t>})

而整體的 loss function 可以定義為

\mathcal{L}(\hat{y}, y) = \sum_{t=1}^{T_x}\mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})

如此一來，就可以回推並更新 $W_y, b_y, W_a, b_a$

Different types of RNNs

剛剛的網路建立在 $T_x = T_y$ 的狀況下
如果要達成各式不同的 input/output 勢必需要不同的網路形式

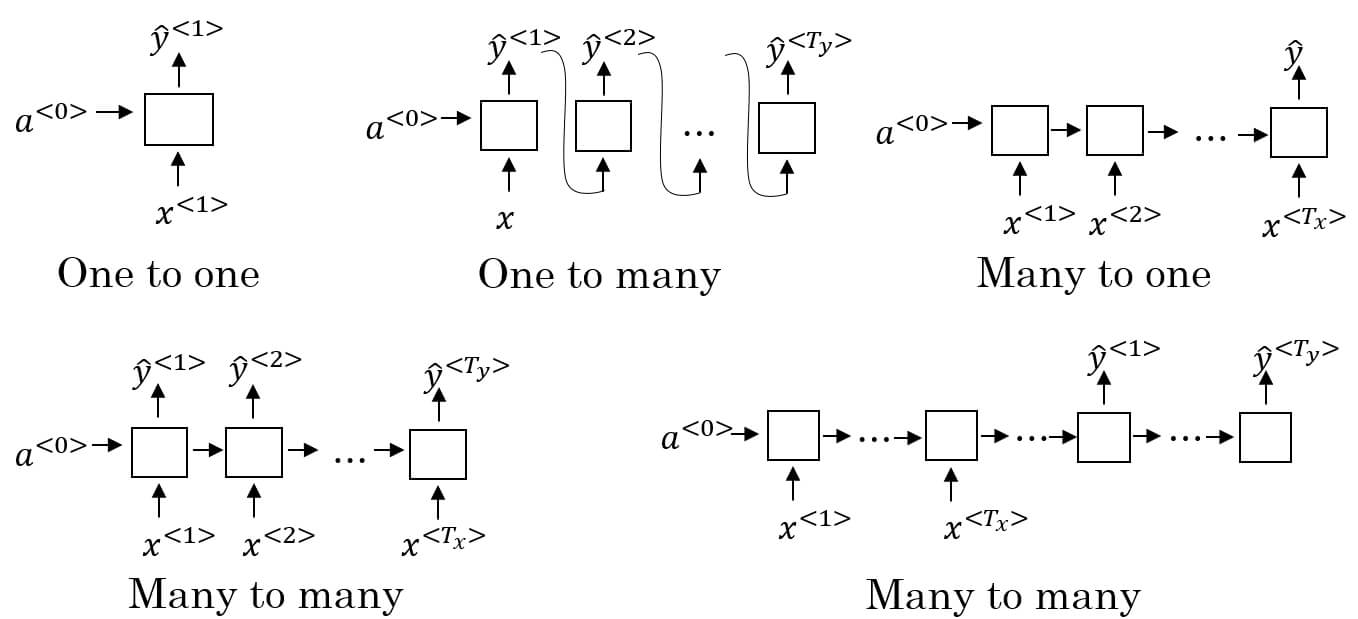
One-to-One
- 很無聊，就是個普通的神經網路
One-to-Many
- 用於 sequence generation
- e.g. music generation
  - 給定音樂種類，生產出一系列的音符
- 要注意的是該種類會把 $\hat{y}$ 當作下一層的 input
Many-to-One
- 用於 sentiment classification
- e.g. 電影評價打分數
  - 讀入一連串的評價，產出 1~5 的分數
Many-to-many with same length
- e.g. name entity recognition
  - 給定一串文字，標示出文字為名稱的部分
Many-to-many with different length
- e.g. machine translation
  - 給定一串英文，翻譯成長度不同的中文
- 首先先讀取 x 的部分，最後再處理 y 的部分

Language model and sequence generation

Language Modelling

假設 speech recognition 時聽到了一句話
- “The apple and pear salad.”
那到底是聽到上面的句子還是 “The apple and pair salad.” ?
為了判斷是哪一句話，所以給兩句話機率的方法就是 language modelling

\begin{aligned} P(\text{The apple and pear salad.}) = 5.7\times 10^{-10}\\ P(\text{The apple and pair salad.}) = 3.2\times 10^{-13} \end{aligned}

可以看到在這個 language model 中
- The apple and pear salad 的機率比較高

Build Language model with RNNs

training set 會是 large corpus of english text
- corpus 是一個 NLP 名詞，代表大量句子所組成的文本
首先要 tokenize corpus 中的所有單字，也就是建立字典
- 標點符號可以 tokenize 可以不要

\begin{aligned} &\text{The } &\text{ Egyptian } &\text{ Mau } &\text{ is } &\text{ a } &\text{ bread } &\text{ of } &\text{ cat }. &\text{ <EOS> }\\ &y^{<1>}&y^{<2>}&y^{<3>}&y^{<4>}&y^{<5>}&y^{<6>}&y^{<7>}&y^{<8>}&y^{<9>} \end{aligned}

tokenize 前有時會增加一個 <EOS> 代表句子結束
tokenize 會將每一個單字轉換為 one hot vector
- 假設有一個 10000 單字的字典，那就會在該單字的 index 設 1 其他設 0
- 今天遇到一個不在字典的單字，例如 Mau
  - 那就會將他設定在 <UNK> 的位置，表示 unknown
Tokenize 後就可以將他們 input 到 RNN 訓練

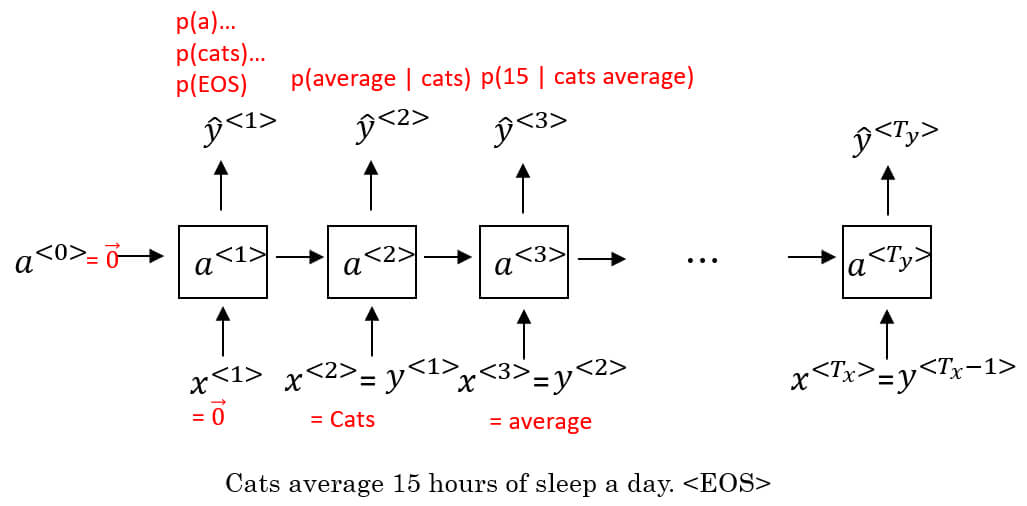
首先 $x^{<1>}$ 和 $a^{<0>}$ 都設為 0
第一個 timestep 算出的 $\hat{y}^{<1>}$ 代表字典中所有單字是句子中第一個字的機率
- 有 10002 個字，包括 EOS 和 UNK $P(\text{a})P(\text{aaron})\cdots P(\text{cat})\cdots P(\text{UNK})P(\text{EOS})$
第二個 timestep 的 $x^{<2>}$ 就是原本句子得到的 $y^{<1>}$
- 加上上一個 timestep 算出的 $a^{<1>}$
- 所以算出來的 $\hat{y}^{<2>}$ 代表出現 cats 後字典裡每一個單字是下一個字的機率
- 所以 average 應該要是最高才對: $P(\text{average}\mid \text{cats}) \text{ should be the highest}$
以此類推， $\hat{y}^{<3>}$ 表示 cats average 出現後，字典中每個單字的出現機率 $P(\text{15} \mid \text{cats average})\text{ should be the highest}$
為了要訓練這個 RNN 我們定義 cost function
- 在 predict 第 t 個單字時的 softmax loss function 為 $\mathcal{L}(\hat{y}^{<t>}, y^{<t>})=-\sum_i y_i^{<t>}\log\hat{y}_i^{<t>}$
- Overall 的 Cost function 為 $\mathcal{L} = \sum_t \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})$
總結一下，要預測一個句子 $P(y^{<1>},y^{<2>},y^{<3>})$ 的機率
- 等於要計算 $P(y^{<1>})$
- 以及知道 $P(y^{<1>})$ 下的 $P(y^{<2>})$ 為何
- 再來是 $P(y^{<1>}, y^{<2>})$ 下 $P(y^{<3>})$ 為何

P(y^{<1>},y^{<2>},y^{<3>}) = P(y^{<1>})P(y^{<2>}\mid y^{<1>})P(y^{<3>}\mid y^{<1>},y^{<2>})

Sampling novel sequences

訓練好的 language model 可以用 sampling 方式來呈現他所學的結果
Sampling 方式就像 one-to-many model
- 給定 $a^{<0>} = x^{<1>} = \vec{0}$
- 算出 $\hat{y}^{<1>}$ 之後，用 np.random.choice 方式從中選取任意一個 sample
- 這個 sample 作為 $x^{<2>}$ 繼續算出 $\hat{y}^{<2>}$ 再選一個 sample
- 以此類推直到 sampling 到 EOS 或是自訂回合數就停止

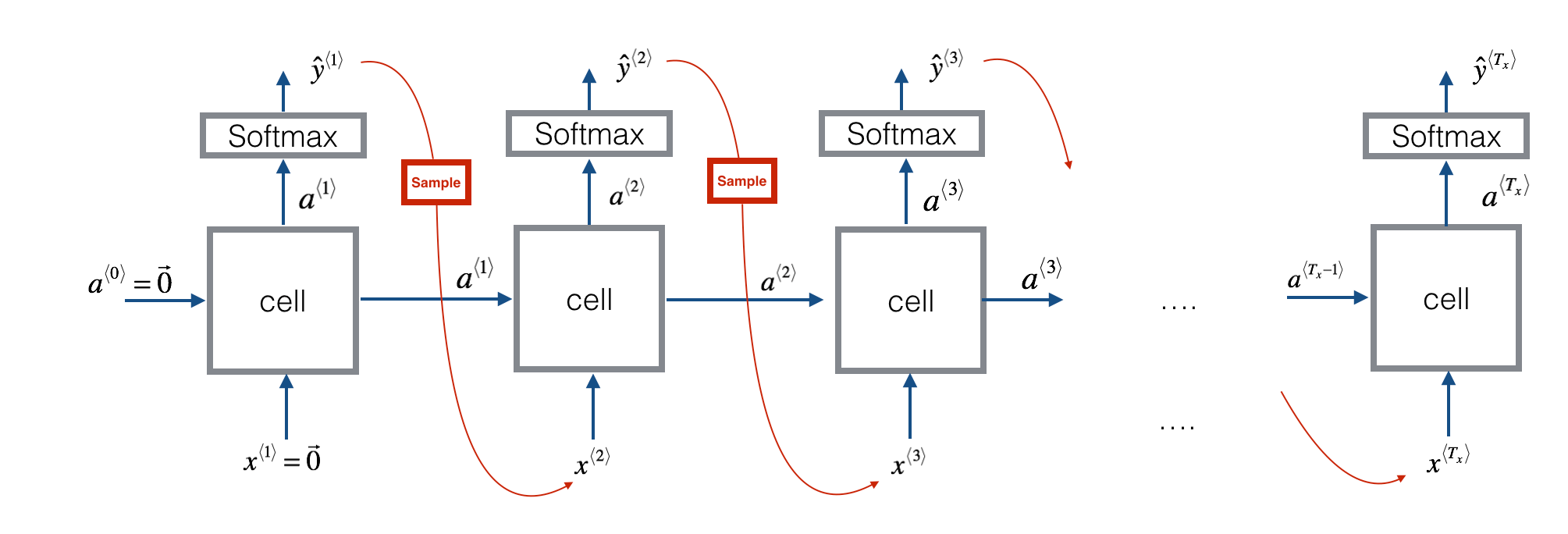
以上的方法每個 $x^{<t>}$ 都是一個單字，稱作 word level model
- $\text{Vocabulary} = [\text{a}, \text{aaron},\cdots, \text{zoo}, \text{<UNK>}]$
我們可以使用 character 作為每個 inputs
- 可以有大小寫字母、數字、符號
- $\text{Vocabulary} = [\text{a, b, c, ..., z, ., ;, 0, ..., 9, A, ...,Z}]$
- 優點是不會有 <UNK>
- 缺點是資料量變大，計算變大、訓練成本過高
  - 不過隨著硬體發展，有一些專案使用 character level model
Sampling example
- 下圖左是一個從 news 訓練出的 model 所產生的 sampling novel sequences
- 下圖右則是讀完沙士比亞文章所產生的 sequences

Vanishing gradients with RNNs

觀察以下兩句句子

\begin{aligned} \text{The cat},\text{ which already ate } \cdots, \text{ was full.} \\ \text{The cats},\text{ which already ate } \cdots, \text{ were full.} \end{aligned}

人類可以記住非常前面的詞 (cat/cats) 來去判斷很後面的詞 (was/were)
但目前的 basic RNN models 很難去找出這種 Long-term Dependencies
原因跟 deep neural networks 已提過的 vanishing gradients 有著很大關係
- 回憶一下 vanishing gradients 是因為 backprop 的導數小於 1
- 造成越往回走梯度越小，最終使得梯度消失

Vanishing gradients in RNNs

RNN 中也有類似 vanishing gradient 的情況，在 RNN 中會出現 local influences
舉例來說 $\hat{y}^{<3>}$ 只會跟 $x^{<1>}, x^{<2>}, x^{<3>}$ 有較大關係
假設 was 在 $\hat{y}^{<100>}$ 那他就無法跟最前面的 cat/cats 互相影響了
這造成 basic RNN model 有著無法處理 long-term dependencies 的弱點

補充

RNN 也有可能出現 Exploding gradient 但情況較少。而且梯度爆炸比較好偵錯，只要參數有問題或是出現 numerial overflow (出現 NaN) 就會知道，並且可以用 gradient clipping 方法解決 (設定 threshold 避免梯度繼續增高)

為了處理 RNN 中的 vanishing gradient，要使用 GRU 及 LSTM 的技術

Notation​

Vocabulary (Dictionary)​

Recurrent Neural Network Model​

Why not standard network ?​

RNNs​

Simplify Forward Propogation​

Backpropogation through time​

Different types of RNNs​

Language model and sequence generation​

Language Modelling​

Build Language model with RNNs​

Sampling novel sequences​

Vanishing gradients with RNNs​

Vanishing gradients in RNNs​