跳至主要内容

Deep Neural Network

Deep neural network 是一種有較多 hidden layers 的神經網路，它能夠對輸入的資料進行複雜的運算，例如人臉辨識、語音辨識等。在一個 deep neural network 中，會使用到越來越複雜的計算，而且每一層的運算結果都會被 cache 起來給下一層使用，從而逐步把複雜的運算細分成簡單的步驟，有效的加速計算的效率。

Deep L-layer Neural Network​

只有 1-layer 的 logistic 及一些層數較少的 nn 會稱作 shallow neural network，而當你有越多的 hidden layers 代表你的 nn 越接近 deep neural network。

首先先介紹一些 deep neural networks 的 notation：LL 表示 layer 數，n[l]n^{[l]} 表示第 l 層的 units 有幾個，a[l]a^{[l]} 表示第 l 層的 activations，且 a[l]=g[l](z[l])a^{[l]} = g^{[l]}(z^{[l]})，w[l]w^{[l]} 和 b[l]b^{[l]} 表示 z[l]z^{[l]} 的 weights。

補充

x=a[0]x = a^{[0]} 表示 input layer，共有 n[0](nx)n^{[0]} (n_x) 個 units；y^=a[L]\hat{y} = a^{[L]} 表示 output layer，共有 n[L]n^{[L]} 個 units。

Forward Propogation in a Deep Neural Network​

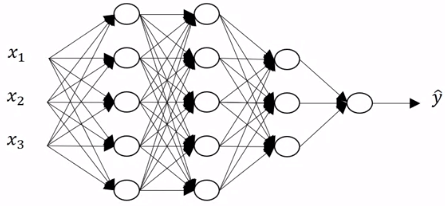5-layer neural network
5-layer neural network

要對五層神經網路進行前向傳播，方法跟之前學的兩層很像，只是不斷對下面這個步驟迭代而已。下面是一個一般化的前向傳播步驟。

Z[l]=W[l]A[l−1]+b[l]X=A[0]A[l]=g[l](Z[l])\begin{aligned} Z^{[l]} &= W^{[l]}A^{[l-1]} + b^{[l]} && X = A^{[0]}\\ A^{[l]} &= g^{[l]}(Z^{[l]}) \end{aligned}

通常若有 l 層，就需要用 for i = 1:l 的 for-loops 而非向量化來遍歷所有層。

Getting your matrix dimensions right (Debug)​

建置一個 nn 時，考慮好每一個 vector 及 matrix 的 dimension 是防止 program 產生問題的重點。

Parameters W[l]W^{[l]} and b[l]b^{[l]}​

5-layer neural network
5-layer neural network
  • 先看計算第一層 zz 時 ww 和 bb 的 dimension
z[1]=w[1]×x+b[1](3,1)(3,2)(2,1)(3,1)(n[1],1)(n[1],n[0])(n[0],1)(n[1],1)\begin{aligned} &z^{[1]} = &w^{[1]} &\times &x &+ &b^{[1]}\\ &(3, 1) &(3, 2) & &(2, 1) & &(3, 1)\\ &(n^{[1]}, 1) &(n^{[1]}, n^{[0]}) & &(n^{[0]}, 1) & &(n^{[1]}, 1) \end{aligned}
  • 可以一般化 ww 和 bb 在計算 zz 時的 dimension
  • 在 backprop 時，產生的 dw,dbdw, db 也會和 w,bw, b 一模一樣 dimension
w[l]=(n[l],n[l−1])b[l]=(n[l],1)=z[l]\begin{aligned} w^{[l]} &= (n^{[l]}, n^{[l-1]}) \\ b^{[l]} &= (n^{[l]}, 1) = z^{[l]} \end{aligned}

Vectorized Implementation​

  • 使用 vectorization 一次執行 m 筆 training examples 於 forward propogation 時
  • 原本的 z 變成一個 m columns 的矩陣
Z[1]=[∣∣∣z[1](1)z[1](2)⋯z[1](m)∣∣∣]Z^{[1]} = \begin{bmatrix} |&|&&|\\ z^{[1](1)}&z^{[1](2)}&\cdots&z^{[1](m)}\\ |&|&&| \end{bmatrix}
  • z 的運算變成這樣
    • b 保持不變是因為 python 會自動使用 broadcasting 技巧
Z[1]=W[1]×X+b[1](n[1],m)(n[1],n[0])(n[0],m)(n[1],1)\begin{aligned} &Z^{[1]} = &W^{[1]} &\times &X &+ &b^{[1]}\\ &(n^{[1]}, m) &(n^{[1]}, n^{[0]}) & &(n^{[0]}, m) & &(n^{[1]}, 1) \end{aligned}
  • z,az, a 變成 Z,AZ, A 在 dimension 上就是從 1 column 變成 m columns
z[l],a[l]:(n[l],1)→Z[l],A[l]:(n[l],m)z^{[l]}, a^{[l]} : (n^{[l]}, 1) \rightarrow Z^{[l]}, A^{[l]} : (n^{[l]}, m)

Why Deep Representations ?​

以下用兩個方向來解釋為什麼 nn 越 deep 越好

Intuition​

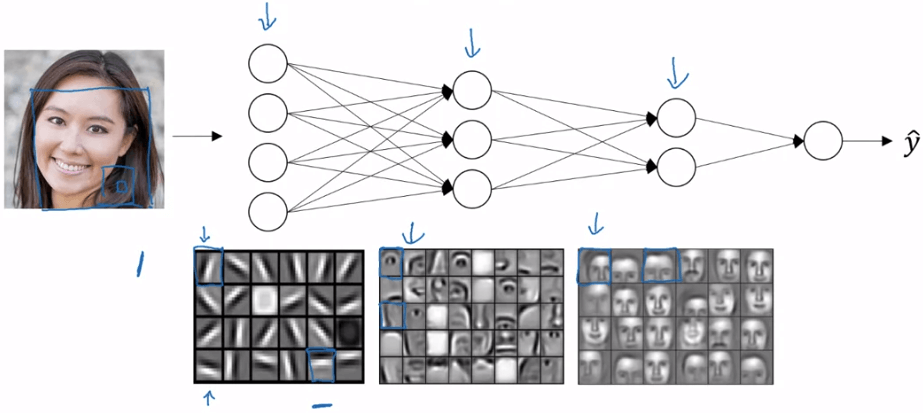Deep neural network intuition
Deep neural network intuition

我們有了 Deep Neural Network，可以對圖片做簡單的運算和偵測，例如找出圖片的水平或垂直邊緣線。然後，我們可以組合上一層的結果，再在下一層進一步運算，例如找出五官或某個部位。越往下層走，就可以得到越複雜的計算，最後可以做到人臉辨識。

另一個例子是語音辨識系統，從 Audio 到 low level audio waves，再到 phonemes、words 和 sentences。因此，Deep Learning 能夠將一個從簡單到複雜的問題，做出近似的解決方案。

Circuit Theory​

另一個例子是用邏輯電路來呈現，假設我要運算出 x1 XOR x2 XOR x3 XOR ⋯ XOR xnx_1 \text{ XOR } x_2 \text{ XOR } x_3 \text{ XOR } \cdots \text{ XOR } x_n，一般的做法都會是使用一個 Olog⁡(N)O\log(N) 的方法 (deep nn 的好處)

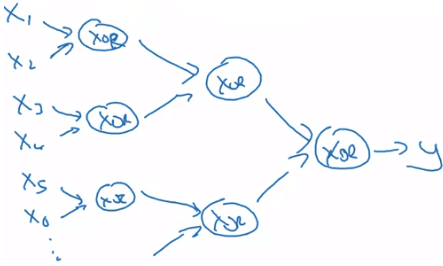Deep learning circuit theory
Deep learning circuit theory
  • 另一種 shallow 的方法則需要展開 O(2N)O(2^N) 的 nodes 才能做到
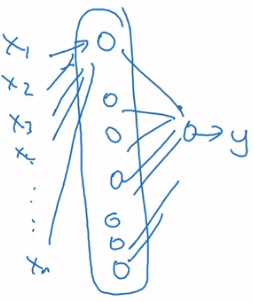Deep learning circuit theory
Deep learning circuit theory
提示

Informally:

  • There are functions you can compute with a "small" L-layer deep neural network
  • that shallower networks require exponentially more hidden units to compute.

Building Blocks of Deep Neural Networks​

  • 在實際建置 dnn 時，可以把每一個 A[l]→A[l+1]A^{[l]} \rightarrow A^{[l+1]} 的 forward 想成一個 block
  • 同理的，也可以將 dA[l−1]←dA[l]dA^{[l-1]} \leftarrow dA^{[l]} 的 backward 想成一個 block
  • forward 會將計算好的值 cache 起來給 backward 使用
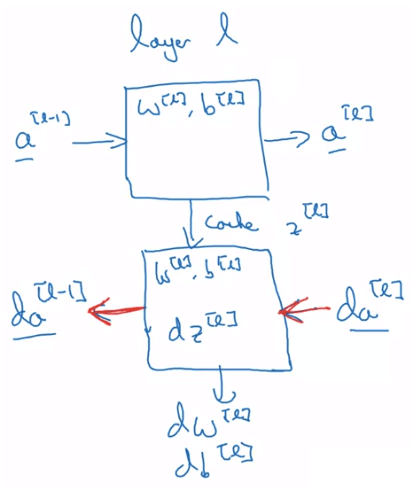Single block of NN
Single block of NN

Forward Propogation​

  • Input : a[l−1]a^{[l-1]}
  • Output : a[l]a^{[l]}
  • Cache : z[l],w[l],b[l]z^{[l]}, w^{[l]}, b^{[l]}
  • Process :
Z[l]=W[l]⋅A[l−1]+b[l]A[l]=g[l](Z[l])\begin{aligned} Z^{[l]} &= W^{[l]} \cdot A^{[l-1]} + b^{[l]} \\ A^{[l]} &= g^{[l]}(Z^{[l]}) \end{aligned}

Backward Propogation​

  • Input : da[l]da^{[l]}
  • Output : da[l−1],dW[l],db[l]da^{[l-1]}, dW^{[l]}, db^{[l]}
  • Process :
dZ[l]=dA[l]⋅∗g[l]′(Z[l])dW[l]=1mdZ[l]⋅A[l−1]Tdb[l]=1mnp.sum(dZ[l])dA[l−1]=W[l]T⋅dZ[l]\begin{aligned} dZ^{[l]} &= dA^{[l]} \cdot \ast g^{[l]'}(Z^{[l]}) \\ dW^{[l]} &= \frac{1}{m} dZ^{[l]} \cdot A^{[l-1]T} \\ db^{[l]} &= \frac{1}{m} \text{np.sum}(dZ^{[l]}) \\ dA^{[l-1]} &= W^{[l]T} \cdot dZ^{[l]} \end{aligned}
  • 整個組合起來的 blocks 會長成這樣
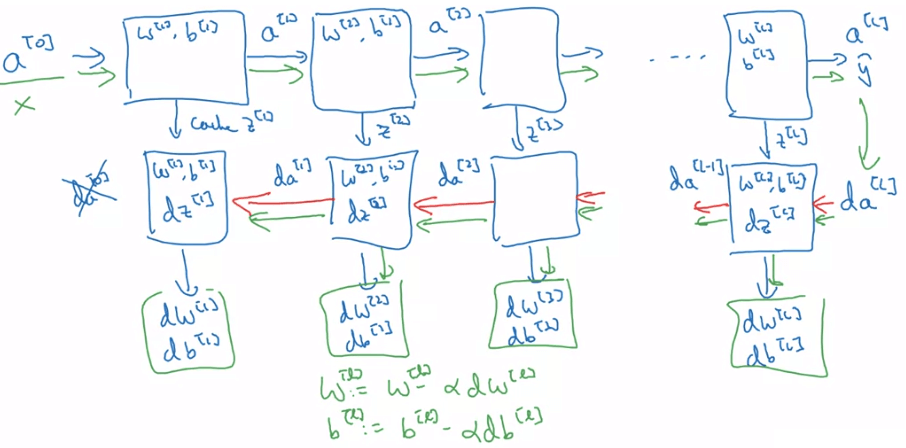DNN blocks
DNN blocks

HyperParameters​

一般的 parameters 是指 W[1],b[1],W[2],b[2],⋯W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}, \cdots，而 hyperparameters 指的是那些足以影響 parameters 的參數，其設定往往需要依靠著經驗，例如：

  • learning rate α\alpha
  • number of iterations
  • number of hidden layers LL
  • number of hidden units n[1],n[2],⋯n^{[1]}, n^{[2]}, \cdots
  • choice of activation functions tanh, ReLU,
  • momentum
  • mini-batch size
  • regularization algorithms 等

因此 deep learning application 其實是一個非常 empirical 的過程，需要不斷的循環於 Idea -> Code -> Experiment 之間。