跳至主要内容

Shallow Neural Network

Shallow Neural Network 指的是只有幾層 (2 層或以下) 的神經網路 (Neural Network)。它們只有輸入層 (input layer) 和輸出層 (output layer)，通常在中間有一層隱藏層 (hidden layer)。它們常用於一些簡單的機器學習任務，例如垃圾郵件分類，激活函數 (activation function) 通常會用 Sigmoid、Tanh 或 ReLU 來替代線性激活函數。激活函數是一種用於增強神經網路計算能力的函數，為了能夠計算 gradient descent (backpropogation)，需要知道每個 activation function 的導數為何，比如 Sigmoid、Tanh、ReLU 和 Leaky ReLU，其導數可以用微分技巧來計算。此外，為了避免所有 weight 初始化全部為 0 的問題，我們會使用隨機取值來初始化 weights。

Neural Network Representation​

Neural Network Representation
Neural Network Representation
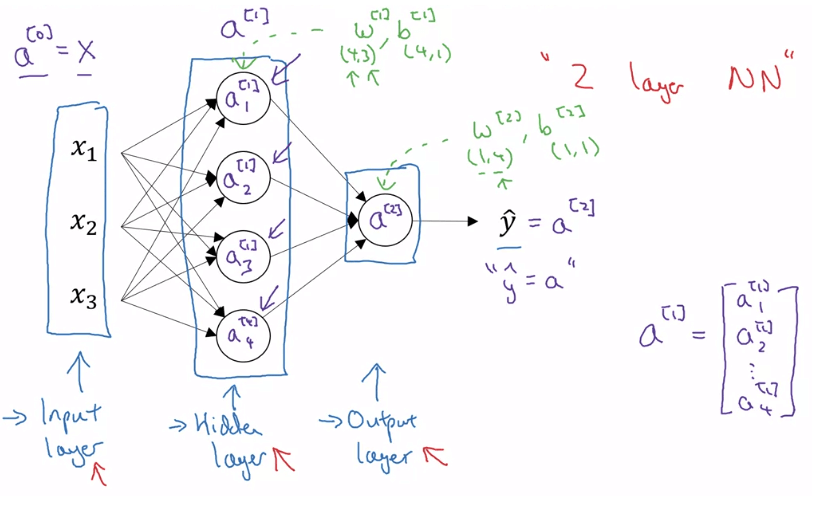
  • 一個 nn 會有 input, hidden, output layer
    • 因為 training set 不包含 hidden layer 的資訊所以得名
    • 在說明 layer 數時，通常不會包含 input layer
  • Notation aa
    • 所有 superscript [i][i] 用來表示第 ii layer
    • 第一層的 aa 就是 a1[1],a2[1],a3[1],a4[1]a^{[1]}_1, a^{[1]}_2, a^{[1]}_3, a^{[1]}_4
    • input xx 會用 a[0]a^{[0]} 表示
  • Notation w,bw, b
    • 除了 input 以外，每一層都會有 w,bw, b 這些 parameters
    • parameter ww 的 dimension 會是 current layer nodes by parent layer nodes
      • w[1]=(4,3)w^{[1]} = (4, 3)
    • parameter bb 的 dimension 會是 current layer nodes by 1\
      • b[1]=(4,1)b^{[1]} = (4, 1)

Computing a Neural Network's Output​

  • 一個 neuron 裡的運算可以拆成 z 和 a
  • 一個 4 unit 的 layer 就要算四次 z 和四次 a
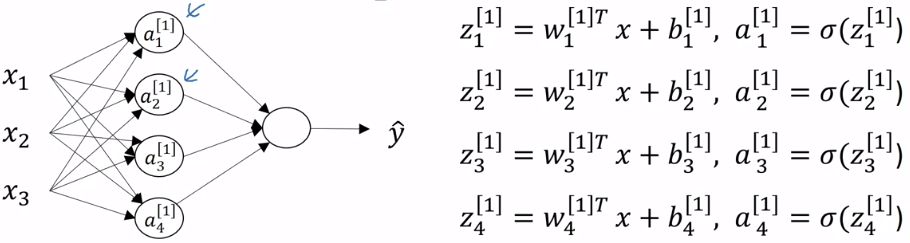
Computing a Neural Network's Output
Computing a Neural Network's Output
  • z 和 a 的運算都可以向量化
  • z[1]=(w[1]T)X=[w1[1]Tw2[1]Tw3[1]Tw4[1]T][x1x2x3]+bz^{[1]} = (w^{[1]T})X = \begin{bmatrix}w_1^{[1]T}\\w_2^{[1]T}\\w_3^{[1]T}\\w_4^{[1]T}\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} + b
    • 裡面的 w[1]w^{[1]} 就是一個 4 * 3 的矩陣
  • a[1]=σ(z[1])a^{[1]} = \sigma(z^{[1]})
  • 另外我們可以用 a[0]a^{[0]} 來表示 XX
  • 所以計算 y^\hat{y} (forward propogation) 的運算如下

z[1]=W[1]a[0]+b[1]a[1]=σ(z[1])z[2]=W[2]a[1]+b[2]a[2]=σ(z[2])\begin{aligned}z^{[1]} &= W^{[1]}a^{[0]}+b^{[1]} \\a^{[1]} &= \sigma(z^{[1]}) \\ z^{[2]} &= W^{[2]}a^{[1]}+b^{[2]} \\a^{[2]} &= \sigma(z^{[2]})\end{aligned}

Vectorizing Across Multiple Examples​

  • 我們有 1 到 m 個 training examples
  • 若用 for-loops 來計算每一個 example 對應的 y^\hat{y}
    • 裡面的 a[2](1){a^[2](1)} 代表第 1 筆 example 的 layer 2 的 a 向量
x(1)→a[2](1)=y^(1)x(2)→a[2](2)=y^(2)⋮x(m)→a[2](m)=y^(m)\begin{aligned} &x^{(1)} \rightarrow a^{[2](1)} = \hat{y}^{(1)} \\ &x^{(2)} \rightarrow a^{[2](2)} = \hat{y}^{(2)} \\ \vdots \\ &x^{(m)} \rightarrow a^{[2](m)} = \hat{y}^{(m)} \end{aligned}
  • 我們的目標其實就是用 nx * m 的 XX 矩陣
  • 來算出 1 m 的 ZZ 矩陣，再求出同樣為 1 m 的 AA 矩陣
  • 橫軸的 m 代表有 m 筆 examples
  • 縱軸的 n 代表有 n 筆 hidden units
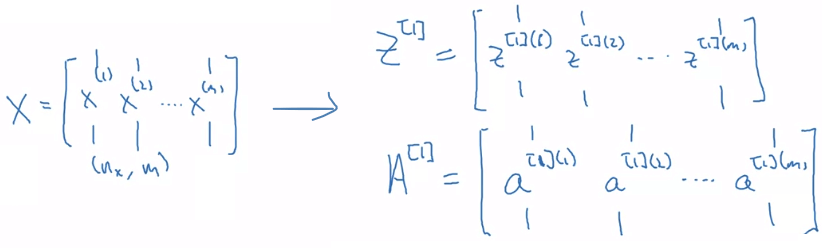
Vectorizing Across Multiple Examples
Vectorizing Across Multiple Examples
  • 整個 vectorize 的 forward propogation 過程
Z[1]=W[1]X+b[1]A[1]=σ(Z[1])Z[2]=W[2]A[1]+b[2]A[2]=σ(Z[2])\begin{aligned} Z^{[1]} &= W^{[1]}X + b^{[1]} \\ A^{[1]} &= \sigma(Z^{[1]}) \\ Z^{[2]} &= W^{[2]}A^{[1]} + b^{[2]} \\ A^{[2]} &= \sigma(Z^{[2]}) \end{aligned}

Activation Functions​

  • Activation function 會影響到 gradient descent 的速度
    • 例如 sigmoid 在大於或小於一定數字後 slope 就會接近 0
    • 所以 sigmoid 並不是最好的 activation function
    • 但 sigmoid 可以用於 logistic regression 的最後一層 output (0, 1)
  • tanh 是一個可以取代 sigmoid 的選擇
    • 他就是 sigmoid 的位移，區間變成 [-1, 1]
    • 因為平均值變為 0 的關係，有集中 data 的效果
    • ez−e−zez+e−z\frac{e^z-e^{-z}}{e^z+e^{-z}}
Tanh
Tanh
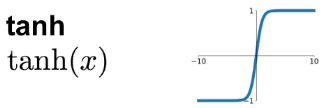
  • ReLU 是現在所有人公認最好的 activation function
    • 如果你不知道該用什麼在 hidden layer，用 ReLU 就對了
    • 他解決了 sigmoid 在一些數字越大時，slope 越小的問題
    • 雖然在負數時，導數皆為 0，但是是沒問題的
ReLU
ReLU
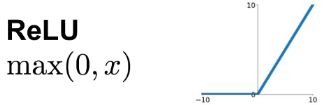
  • Leaky ReLU 是 ReLU 的變形
    • 修正了負數導數為 0 的問題
    • 但一般來說，使用 ReLU 就夠了
Leaky ReLU
Leaky ReLU

Why Non-linear Activation Functions​

  • 若你把某一層 hidden layer 的 activation function 全部取消掉
  • 輸入會永遠等於輸出，這稱為 linear activation function
  • 若使用 linear activation function 則該層的運算會跟沒算一樣
    • hidden layer 有跟沒有一樣
  • 甚至在所有 hidden 使用 linear，而最後一層使用 sigmoid 時
    • 算出來的效果比 logistic regression 還要差

Derivatives of Activation Functions​

  • 為了能夠計算 gradient descent (backpropogation)，需要知道每個 activation function 的導數為何
  • Sigmoid 為 g(z)=11+e−zg(z) = \frac{1}{1+e^{-z}}
    • 他的導數如下，需要用到一些微分技巧
      • ddzg(z)=11+e−z(1−11+e−z)g′(z)=g(z)(1−g(z))\begin{aligned}\frac{d}{dz}g(z) &= \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})\\\\g'(z)&=g(z)(1-g(z))\end{aligned}
  • Tanh 為 g(z)=ez−e−zez+e−zg(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}}
    • 他的導數如下，一樣需要用到微分技巧
      • g′(z)=1−(tanh⁡(z))2g'(z) = 1 - (\tanh(z))^2
    • 在 nn 中我們會以 a=g(z)a = g(z) 表示，所以微分也可寫成以下
      • g′(z)=1−a2g'(z) = 1 - a^2
  • ReLU 為 g(z)=max⁡(0,z)g(z) = \max(0, z)
    • 他的導數如下
      • g′(z)={0if z<01if z≥0g'(z) = \left\{\begin{matrix}0&\text{if } z < 0\\1 &\text{if }z \ge 0\end{matrix}\right.
      • 當 z=0z = 0 時雖然為 undefined，但在電腦中可以自行決定要等於 0 或 1
      • 其實沒有太大影響
  • Leaky ReLU 為 g(z)=max⁡(0.01z,z)g(z) = \max(0.01z, z)
    • 他的導數如下
      • g′(z)={0.01if z<01if z≥0g'(z) = \left\{\begin{matrix}0.01&\text{if } z < 0\\1 &\text{if }z \ge 0\end{matrix}\right.

Gradient Descent for Neural Networks​

  • 假設有一個 2-layer nn
  • input, hidden, output units 的數量，分別為 n[0],n[1],n[2]n^{[0]}, n^{[1]}, n^{[2]}
  • Parameters 有 w[1],b[1],w[2],b[2]w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}
    • w[1]=n[1]×n[0]w^{[1]} = n^{[1]} \times n^{[0]}
    • b[1]=n[1]×1b^{[1]} = n^{[1]} \times 1
    • w[2]=n[2]×n[1]w^{[2]} = n^{[2]} \times n^{[1]}
    • b[2]=n[2]×1b^{[2]} = n^{[2]} \times 1
  • 然後 Cost Function 為 1m∑i=1nL(y^,y)\frac{1}{m}\sum_{i=1}^n\mathcal{L}(\hat{y}, y)
  • 所以 Gradient Descent 大致上運作如下
Repeat : Compute predicts (y^(i),i=1⋯m)dw[1]=∂J∂w[1],db[1]=∂J∂b[1]w[1]=w[1]−αdw[1],b[1]=b[1]−αdb[1]dw[2]=∂J∂w[2],db[2]=∂J∂b[2]w[2]=w[2]−αdw[2],b[2]=b[2]−αdb[2]\begin{aligned} \text{Repeat : } &\\ &\text{Compute predicts } (\hat{y}^{(i)}, i = 1 \cdots m)\\ &dw^{[1]} = \frac{\partial J}{\partial w^{[1]}}, db^{[1]} = \frac{\partial J}{\partial b^{[1]}} \\ &w^{[1]} = w^{[1]} - \alpha dw^{[1]}, b^{[1]} = b^{[1]} - \alpha db^{[1]}\\ &dw^{[2]} = \frac{\partial J}{\partial w^{[2]}}, db^{[2]} = \frac{\partial J}{\partial b^{[2]}} \\ &w^{[2]} = w^{[2]} - \alpha dw^{[2]}, b^{[2]} = b^{[2]} - \alpha db^{[2]} \end{aligned}
  • 接著我們要深入一點，在公式中解出 dw[1]=∂J∂w[1]dw^{[1]} = \frac{\partial J}{\partial w^{[1]}} 這些導數
  • 以下是一個已經 vectorized 的 backpropogation formula
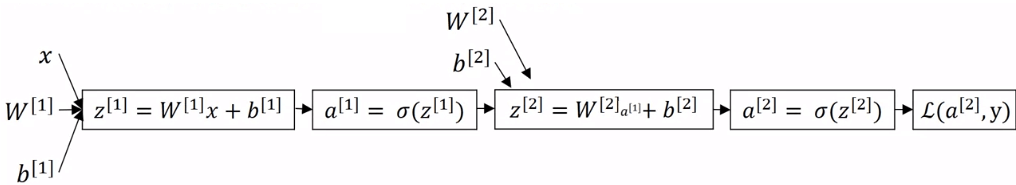
Neural Network 2-layer Computation Graph
Neural Network 2-layer Computation Graph
dZ[2]=A[2]−Y(sigmoid)Y=[y(1)⋯y(m)]dW[2]=1mdZ[2]⋅A[1]Tdb[2]=1mnp.sum(dZ[2],axis=1, keepdims=True)dZ[1]=W[2]TdZ[2]⋅∗g[1]′(Z[1])dW[1]=1mdZ[1]⋅XTdb[1]=1mnp.sum(dZ[1],axis=1, keepdims=True)\begin{aligned} dZ^{[2]} &= A^{[2]} - Y (\text{sigmoid})&& Y = [y^{(1)} \cdots y^{(m)}]\\ dW^{[2]} &= \frac{1}{m}dZ^{[2]}\cdot A^{[1]T}\\ db^{[2]} &= \frac{1}{m}\text{np.sum}(dZ^{[2]},\text{axis=1, keepdims=True})\\ dZ^{[1]} &= W^{[2]T} dZ^{[2]} \cdot * g^{[1]'}(Z^{[1]})\\ dW^{[1]} &= \frac{1}{m}dZ^{[1]}\cdot X^T\\ db^{[1]} &= \frac{1}{m}\text{np.sum}(dZ^{[1]},\text{axis=1, keepdims=True}) \end{aligned}
  • 第四行的 dZ[1]=W[2]TdZ[2]⋅∗g[1]′(Z[1])dZ^{[1]} = W^{[2]T} dZ^{[2]} \cdot * g^{[1]'}(Z^{[1]}) 是怎麼來的
  • 我們可以寫成 chain rule
∂L∂Z[1]=∂L∂A[2]⋅∂A[2]∂Z[2]⋅∂Z[2]∂A[1]⋅∂A[1]∂Z[1]\frac{\partial L}{\partial Z^{[1]}}= \color{red}{\frac{\partial L}{\partial A^{[2]}}\cdot \frac{\partial A^{[2]}}{\partial Z^{[2]}}}\cdot \color{green}{\frac{\partial Z^{[2]}}{\partial A^{[1]}}\cdot} \color{blue}{\frac{\partial A^{[1]}}{\partial Z^{[1]}}}
  • 紅色部份就是 dLdZ[2]=dZ[2]\color{red}{\frac{dL}{dZ^{[2]}} = dZ^{[2]}}
  • 綠色部份就是 Z[2] at A[1]Z^{[2]} \text{ at } A^{[1]} 的導數，等於 W[2]\color{green}{W^{[2]}}
  • 最後藍色部份是 A[1] at Z[1]A^{[1]} \text{ at } Z^{[1]} 的導數，等於 g[1]′(Z[1])\color{blue}{g^{[1]'}(Z^{[1]})}
備註

See the full derivatives here

Random Initialization​

  • 在 machine learning 中提過，若 weightsweights 初始全為 0
    • 會讓整個 layer 全部都做一樣的事情
  • 所以在初始化 nn 的 weights 時，會使用隨機取值
  • b 可以初始為 0 沒關係
  • 以下是用 python 進行 random initialization 的動作
w1 = np.random.randn(2, 2) * 0.01
b1 = np.zeros(2, 1)
w2 = ...
b2 = ...
...