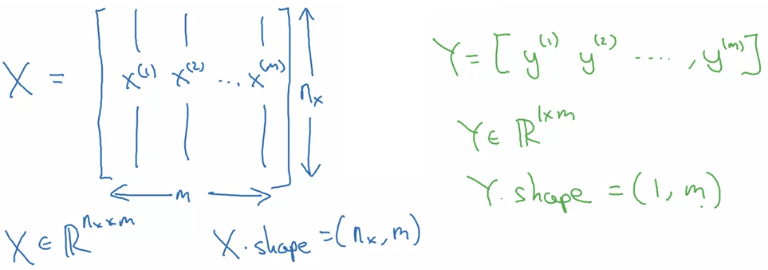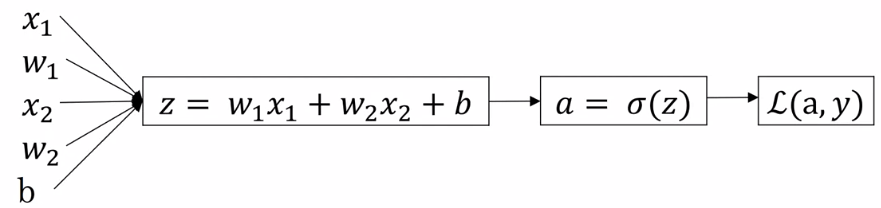Logistic Regression as a NN 這篇文章將介紹如何將 Logistic Regression 抽象化為一個 Neural Network 。我們將以一個 Binary Classification 的問題來說明,藉由 Neural Network 來辨別一張 64x64 的圖片是否是貓。我們會定義一個 Loss Function 來作為 training set 的誤差,並且將所有的 training sets 集合形成 Cost Function,再利用 Gradient Descent 來優化參數,以達到最小化 Cost Function。最後我們會介紹如何利用 Computation Graph 來加速參數的更新,以及 Backpropogation 的運算細節。
一開始,我們想將一張 64x64 的圖片餵進神經網路中,來辨識是否是貓,1 代表是,0 代表不是,怎麼餵呢,我們將圖片中 RGB 三種顏色 channel 的各 64x64 個像素存到一個非常長的向量 x,共有 12288 個特徵。
x = [ 255 231 ⋮ 255 134 ⋮ 255 134 ⋮ ] \begin{aligned} x = \begin{bmatrix} 255\\231\\\vdots\\255\\134\\\vdots\\255\\134\\\vdots \end{bmatrix} \end{aligned} x = ⎣ ⎡ 255 231 ⋮ 255 134 ⋮ 255 134 ⋮ ⎦ ⎤ 我們會使用 n x n_x n x n = n x = 12288 n = n_x = 12288 n = n x = 12288
我們的 training sets 為 ( x , y ) (x, y) ( x , y )
x ∈ R n x , y ∈ { 0 , 1 } x \in \mathbb{R}^{n_x}, y \in \begin{Bmatrix}0,1\end{Bmatrix} x ∈ R n x , y ∈ { 0 , 1 } 共有 m 個 training sets
{ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) } \begin{Bmatrix}(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}),\cdots, (x^{(m)}, y^{(m)})\end{Bmatrix} { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) } 並且我們會壓縮所有的 training sets 和 y 成為一個大矩陣,這邊跟 machine learning 學的有點不一樣:
在 X X X x ( i ) x^{(i)} x ( i ) x x x y y y y ( i ) y^{(i)} y ( i )
Binary Classification Notation 定義好 x x x y ^ \hat{y} y ^ w ∈ R n x w \in \mathbb{R}^{n_x} w ∈ R n x b ∈ R b \in \mathbb{R} b ∈ R
Given x ∈ R n x , want y ^ = P ( y = 1 ∣ x ) , 0 ≤ y ^ ≤ 1 \text{Given } x \in \mathbb{R}^{n_x},\text{ want } \hat{y} = P(y=1\mid x), 0 \le \hat{y} \le 1 Given x ∈ R n x , want y ^ = P ( y = 1 ∣ x ) , 0 ≤ y ^ ≤ 1 w w w θ \theta θ b b b θ 0 \theta_0 θ 0 y ^ \hat{y} y ^ h θ ( x ) h_\theta(x) h θ ( x ) σ \sigma σ g g g
y ^ = σ ( w T x + b ) \hat{y} = \sigma(w^Tx + b) y ^ = σ ( w T x + b ) 我們會定義一個 Loss function 來當作 single training set 的誤差
L ( y ^ , y ) = − ( y log y ^ + ( 1 − y ) log ( 1 − y ^ ) ) \mathcal{L}(\hat{y}, y) = -(y\log \hat{y} + (1-y)\log (1-\hat{y})) L ( y ^ , y ) = − ( y log y ^ + ( 1 − y ) log ( 1 − y ^ )) 以下是一個 intuition 為什麼這個 loss function 可以這樣定義
If y = 1 : L ( y ^ , y ) = − log y ^ If y = 0 : L ( y ^ , y ) = − log ( 1 − y ^ ) \begin{aligned} &\text{If } y = 1 : && \mathcal{L}(\hat{y}, y) = -\log \hat{y} \\ &\text{If } y = 0 : && \mathcal{L}(\hat{y}, y) = -\log(1 - \hat{y}) \end{aligned} If y = 1 : If y = 0 : L ( y ^ , y ) = − log y ^ L ( y ^ , y ) = − log ( 1 − y ^ ) 當 y y y y ^ \hat{y} y ^ y ^ \hat{y} y ^ y y y − log y ^ ≈ 0 -\log \hat{y} \approx 0 − log y ^ ≈ 0
當 y y y y ^ \hat{y} y ^ − log ( 1 − y ^ ) -\log(1 - \hat{y}) − log ( 1 − y ^ )
於是我們可以將作用在每一筆 training sets 的 loss function 集合形成 cost function J ( w , b ) J(w,b) J ( w , b )
cost function is the average of the loss functions of the entire training set
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] \begin{aligned} J(w,b) &= \frac{1}{m}\sum_{i=1}^m\mathcal{L}(\hat{y}^{(i)}, y^{(i)}) \\ &= -\frac{1}{m}\sum_{i=1}^{m}\begin{bmatrix}y^{(i)}\log\hat{y}^{(i)} + (1- y^{(i)}) \log(1-\hat{y}^{(i)})\end{bmatrix} \end{aligned} J ( w , b ) = m 1 i = 1 ∑ m L ( y ^ ( i ) , y ( i ) ) = − m 1 i = 1 ∑ m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] 裡面的 superscript i 代表第 i 個 training set
這邊的 gradient descent 和 machine learning 時學的大同小異,只是現在我們連 b 也要一起進行更新
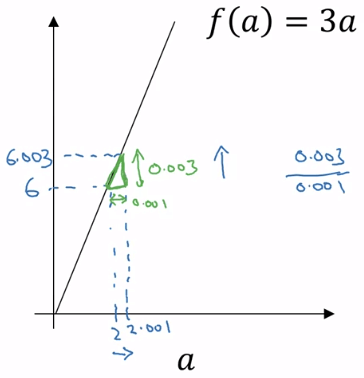
Repeat : w : = w − α ∂ J ( w , b ) ∂ w b : = b − α ∂ J ( w , b ) ∂ b \begin{aligned} &\text{Repeat :} && \\ &&w := w - \alpha \frac{\partial J(w, b)}{\partial w}\\ &&b := b - \alpha \frac{\partial J(w, b)}{\partial b}\\ \end{aligned} Repeat : w := w − α ∂ w ∂ J ( w , b ) b := b − α ∂ b ∂ J ( w , b ) 在探討梯度下降時,我們需要用到微分技巧,以求出對應的成本函數當下的斜率。斜率的計算公式為 height width \frac{\text{height}}{\text{width}} width height f ( a ) = 3 a f(a) = 3a f ( a ) = 3 a
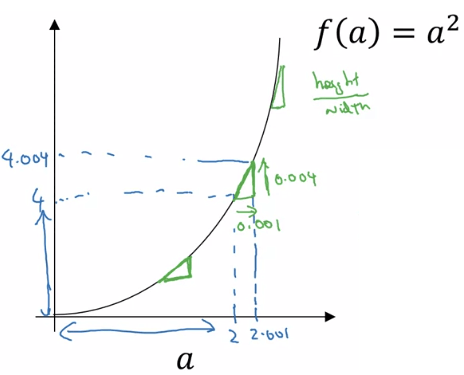
Derivative from Gradient Descent a = 2 f ( a ) = 6 a = 2.001 f ( a ) = 6.003 Slope of f ( a ) at a = 2 is 0.003 0.001 = 3 = ∂ f ( a ) ∂ a \begin{aligned} &a = 2 && f(a) = 6\\ &a = 2.001 && f(a) = 6.003\\ &\text{Slope of } f(a) \text{ at } a = 2 \text{ is } \frac{0.003}{0.001} = 3 = \frac{\partial f(a)}{\partial a} \end{aligned} a = 2 a = 2.001 Slope of f ( a ) at a = 2 is 0.001 0.003 = 3 = ∂ a ∂ f ( a ) f ( a ) = 6 f ( a ) = 6.003 在不同的函數上,斜率可能會不斷變動。例如,在 f ( a ) = a 2 f(a) = a^2 f ( a ) = a 2
a = 2 f ( a ) ≈ 4 a = 2.001 f ( a ) ≈ 4.004 Slope d f ( a ) d a = 4 when a = 2 \begin{aligned} &a = 2 && f(a) \approx 4\\ &a = 2.001 && f(a) \approx 4.004\\ &\text{Slope } \frac{df(a)}{da} = 4 \text{ when } a = 2 \end{aligned} a = 2 a = 2.001 Slope d a df ( a ) = 4 when a = 2 f ( a ) ≈ 4 f ( a ) ≈ 4.004
a = 5 f ( a ) ≈ 25 a = 5.001 f ( a ) ≈ 25.010 Slope d f ( a ) d a = 10 when a = 5 \begin{aligned} &a = 5 && f(a) \approx 25\\ &a = 5.001 && f(a) \approx 25.010\\ &\text{Slope } \frac{df(a)}{da} = 10 \text{ when } a = 5 \end{aligned} a = 5 a = 5.001 Slope d a df ( a ) = 10 when a = 5 f ( a ) ≈ 25 f ( a ) ≈ 25.010
Derivative Changing 可以看到不同地方的三角形所產生的斜率都不同。這其實就是一次微分的意義。常見的有:
f ( a ) = a 2 d f ( a ) d a = 2 a f ( a ) = a 3 d f ( a ) d a = 3 a 2 f ( a ) = ln ( a ) d f ( a ) d a = 1 a \begin{aligned} &f(a) = a^2 && \frac{d f(a)}{da} = 2a\\ &f(a) = a^3 && \frac{d f(a)}{da} = 3a^2\\ &f(a) = \ln(a) && \frac{d f(a)}{da} = \frac{1}{a}\\ \end{aligned} f ( a ) = a 2 f ( a ) = a 3 f ( a ) = ln ( a ) d a df ( a ) = 2 a d a df ( a ) = 3 a 2 d a df ( a ) = a 1
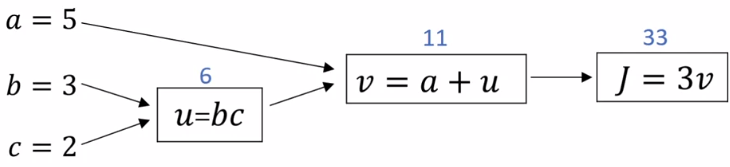
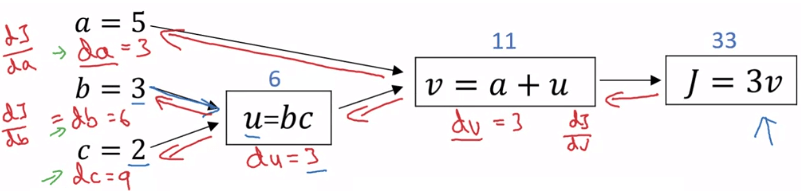
在講解 backpropogation 前,我們先用一個簡單方法來解釋一下流程。假設我們想要最小化 J ( a , b , c ) = 3 ( a + b c ) J(a,b,c) = 3(a+bc) J ( a , b , c ) = 3 ( a + b c )
u = b c v = a + u J = 3 v \begin{aligned} u &= bc\\ v &= a+u\\ J &= 3v \end{aligned} u v J = b c = a + u = 3 v
我們可以將他們畫成底下的 computation graph:
Simple Computation Graph 而 backpropogation 就像是由右往左取每一個數對 J 的導數一樣,求完就可以對每個數做 gradient descent。但是,為什麼要由右往左取呢?因為我們需要用到 chain rule 的關係!
以下會將 d J d v a r \frac{dJ}{dvar} d v a r dJ d v a r dvar d v a r d J d a = d a \frac{dJ}{da} = da d a dJ = d a d J d b = d b \frac{dJ}{db} = db d b dJ = d b
Computation Graph Backpropogation 現在我們就可以往前求得 d v = 3 dv = 3 d v = 3
v = 1 J = 3 v = 1.001 J = 3.003 Slope = 0.003 0.001 = 3 \begin{aligned} &v = 1 && J = 3\\ &v = 1.001 && J = 3.003 \\ &\text{Slope } = \frac{0.003}{0.001} = 3 \end{aligned} v = 1 v = 1.001 Slope = 0.001 0.003 = 3 J = 3 J = 3.003 再來我們再往前求得 d a = 3 da = 3 d a = 3
d J d a = d J d v d v d a = 3 ⋅ d v d a \frac{dJ}{da} = \frac{dJ}{dv} \frac{dv}{da} = 3 \cdot \frac{dv}{da} d a dJ = d v dJ d a d v = 3 ⋅ d a d v 我們已經知道 d J d v \frac{dJ}{dv} d v dJ
a = 5 v = 11 a = 5.001 J = 11.001 Slope = 0.001 0.001 = 1 \begin{aligned} &a = 5 && v = 11\\ &a = 5.001 && J = 11.001 \\ &\text{Slope } = \frac{0.001}{0.001} = 1 \end{aligned} a = 5 a = 5.001 Slope = 0.001 0.001 = 1 v = 11 J = 11.001 所以 d a = d J d a = 3 ⋅ d v d a = 3 ⋅ 1 = 3 da = \frac{dJ}{da} = 3 \cdot \frac{dv}{da} = 3 \cdot 1 = 3 d a = d a dJ = 3 ⋅ d a d v = 3 ⋅ 1 = 3
我們將 logistic regression 計算 cost function 轉換成 computation graph
Logistic Regression Computation Graph 計算 a 的導數為 d a = d L ( a , y ) d a = − y a + 1 − y 1 − a da = \frac{d\mathcal{L}(a, y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a} d a = d a d L ( a , y ) = − a y + 1 − a 1 − y 計算 z 的導數為 d z = d L ( a , y ) d z = d L d a ⋅ d a d z = a − y dz = \frac{d\mathcal{L}(a, y)}{dz} = \frac{d\mathcal{L}}{da} \cdot \frac{da}{dz}= a - y d z = d z d L ( a , y ) = d a d L ⋅ d z d a = a − y 其中已知 d L d a = − y a + 1 − y 1 − a \frac{d\mathcal{L}}{da} = -\frac{y}{a} + \frac{1-y}{1-a} d a d L = − a y + 1 − a 1 − y 而新的 d a d z = a ( 1 − a ) \frac{da}{dz} = a(1-a) d z d a = a ( 1 − a ) 接著就可以算出 w 1 , w 2 , b w_1, w_2, b w 1 , w 2 , b J J J d w 1 = d L d w 1 = x 1 ⋅ d z dw_1 = \frac{d\mathcal{L}}{dw_1} = x_1 \cdot dz d w 1 = d w 1 d L = x 1 ⋅ d z d w 2 = d L d w 2 = x 2 ⋅ d z dw_2 = \frac{d\mathcal{L}}{dw_2} = x_2 \cdot dz d w 2 = d w 2 d L = x 2 ⋅ d z d b = d L d b = d z db = \frac{d\mathcal{L}}{db} = dz d b = d b d L = d z 然後對這三個數做 gradient descentw 1 : = w 1 − α d w 1 w_1 := w_1 - \alpha dw_1 w 1 := w 1 − α d w 1 w 2 : = w 2 − α d w 2 w_2 := w_2 - \alpha dw_2 w 2 := w 2 − α d w 2 b : = b − α d b b := b - \alpha db b := b − α d b 接著我們把上面所有東西統整一起,對 m 筆 training sets 做一次 gradient descent,pseudo code 如下:
J = dw1 = dw2 = db = 0 For i = 1 to m: % 首先是 forward propogation z(i) = w'x(i) + b % 每個 training set 的 z a(i) = sigmoid(z(i)) % 每個 training set 的 a J += -[y(i) * log(a(i)) + (1 - y(i)) * log(1 - a(i))] % 加總所有 training sets 的 cost % 接著是 backward propogation dz(i) = a(i) - y(i) % 每個 training set 的 dz % feature 很多時,這裡會是一個 loop dw1 += x1(i) * dz(i) % 每個 training set 的 dw1 加到一個 dw1 總合去 dw2 += x2(i) * dz(i) % 每個 training set 的 dw2 加到一個 dw2 總合去 db += dz(i) % 每個 training set 的 db 加到一個 db 總合去 % 結束迴圈後對以下幾個東西,都求平均數 J /= m dw1 /= m dw2 /= m db /= m 這個做法可能會用到兩個迴圈,一個是對 m 筆資料,一個是對 n 個 input features (dw1, dw2, ..., dwn),所以下一個章節我們要學習 vectorization 的精神來解決問題。