Hyperparameter, Batch Normalization, Softmax
本文探討了訓練深度學習模型時最常用的兩個觀念,包括調整超參數 (hyperparameter tuning) 以及使用批次正規化 (batch normalization)。文中比較了不同的調整超參數的方法,並列出了調整的區間以及最適當的範圍。文章接著介紹了批次正規化,並說明了在深度學習模型中如何使用批次正規化來加快訓練速度。文中更進一步介紹了 Softmax Regression 以及其 Cost Function 和 Gradient Descent 的用法,並且提及了常見的深度學習框架,以及如何選擇合適的框架以及框架的重要性。
Hyperparameter Tuning
- 下面來 ranking 一下目前所出現過的 hyperparameters 重要度
- 最重要
- Learning rate
- 第二重要
- Momentum parameter
- Number of hidden units
- Mini-Batch size
- 第三重要
- Number of layers
- Learning rate decay
- 不怎麼需要調整
- Adam parameters
Tunning Process
- 我們可以一次測試多種 hyperparameters 的組合
- 但不要使用 grid 當作測試方法
- 假設你的 (x, y) 選用最重要跟最不重要的
- 那麼你用 grid 方式等於只是在測試五種 而已
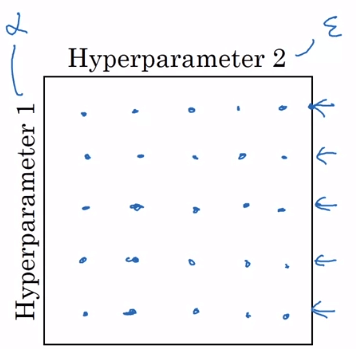
- 隨機選擇測試組合
- 這是相對不錯的測試方法
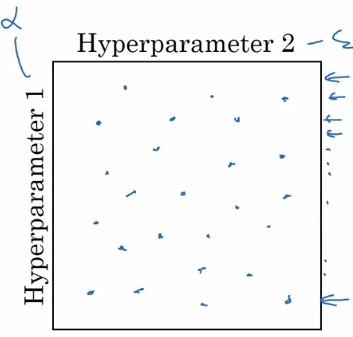
- Coarse to fine
- 基於隨機選擇,在測試時順便聚焦到測試結果不錯的區域,繼續測試該區域
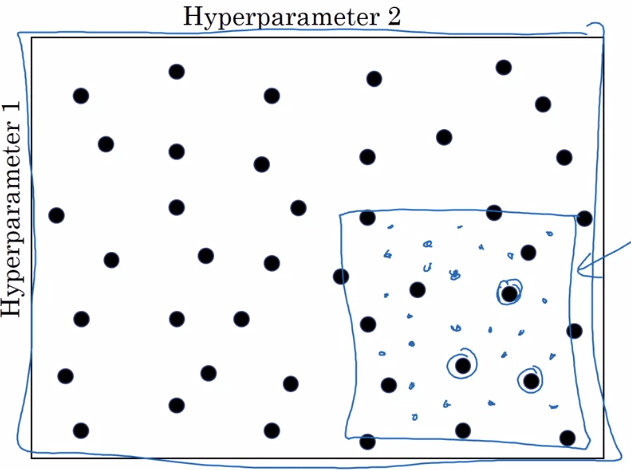
Appropriate Scale for Picking Hyperparameters
- 在隨機選取 hyperparameters 時要注意數值的區間 scale
- 例如隨機選取 layers 或 units,線性區間是非常合理的事
- n = [50, 100], L = [2, 4]
- 但在選取 時,不同區間代表的意義不同
- 例如 從 0.9 增加至 0.9005 幾乎沒影響
- 依然是在取大約前 10 個值的平均
- 但是 從 0.999 增加至 0.9995
- 代表原本取前 1000 個值的平均
- 變成取前 2000 個值的平均
- 例如 從 0.9 增加至 0.9005 幾乎沒影響
- 所以對這些 hyperparameters 必須先依區間拆分,然後再從每個區間隨機取值
- 拆成 0.0001, 0.001, 0.01, 0.1
- 取 然後像 一樣拆成 0.1, 0.01, 0.001
Practices
- 考慮數據、伺服器等環境變化,最好每隔幾個月就要更新你的 hyperparameters,來獲得當前最好的模型
- Deep learning 中,hyperparameters 可能可以跨領域設定,所以時常關注不同領域的應用可以獲得靈感
- 在訓練模型時,有兩種方法
- Panda (babysitting one model)
- 硬體有限、模型困難,所以無法一次測試大量模型時採用
- 快速建置、開始測試、不斷調整參數
- 就像熊貓一樣專心的照顧自己小孩
- Caviar (training many model parallelly)
- 有足夠硬體、自己足以應付多個模型
- 一次平行測試多種 hyperparameters 的結果,並挑選最好的
- 就像魚一次產下上億個魚卵,看看能不能有很棒的小孩出現
- Panda (babysitting one model)
Batch Normalization (BN)
- Batch Normalization (BN) 有許多好處
- 訓練速度提升
- 快速尋找 hyperparameters,所以尋找範圍更加旁大
- 能夠使 NN 不會受 hyperparameters 影響,更加穩定
- 在先前我們學過 Normalize input
- 那我們能不能把這個方法,也運用在每個 hidden layers 的 activation units () 呢 ?
- 答案是可以的,而且能夠加速 的訓練
- 實作時通常會 normalize ,實作如下
- 此時所有新的 的 mean = 0, variance = 1
- 但我們不想讓每個 都一樣是 mean = 0, variance = 1
- 以 sigmoid 為假設,這樣 normalize 後,每一個 都會在 sigmoid 的 linear 區間
- 將會不利於訓練 non-linear neural network,進而得到不好的模型
- 所以我們再次計算
- 這個 跟 一樣都是 parameters,可以隨著 gradient descent 更新
- 最終這個 就可以取代
Adding BN to a NN
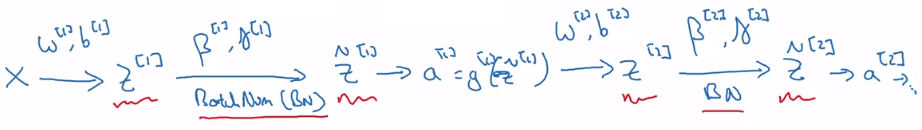
- 所以現在利用 計算完 之後
- 再用 計算 ,以此類推下去
- Backpropogation 一樣就會計算出 來更新
- 另外由於 BN 包含減去 mean 的動作,使得 參數變得沒有作用
- 會變成由 來取代 的工作
- 所以在 BN 中,可以把 省略或設為 0
Why BN works ?
- 因為對每個 neuron 的 input 都做了 normalization,所以提高整體訓練速度
- 因為 normalization 的關係,所有前面層的 weights 對後面層影響減少,更加精確
- 每一層之間的 weights 耦合度減少,所以更加獨立,並提升自我學習的強度
- 減緩了 "Covariate Shift" 的影響
- BN 也起到了些微的 regularization 效果
- 因為是在每個 mini-batch 重新計算 mean, variance
- 這樣計算的結果會產生一些 noise,這些 noise 產生了類似 dropout 的效果
- 若 mini-batch size 越大,這個效果會越小
- 不要把 regularization 當作使用 BN 的主要原因
BN at test time
- BN 能在 mini-batch 時運作良好
- 但在運行 test set 時,資料是一筆一筆出現,無法得到
- 解決方法 : 當訓練每一個 mini-batch 時,會得到每一個
- 將這些參數當成 進行 exponentailly weighted averages
- 預測出最終給 test 時使用的 即可
Softmax Regression
- 要得到多個種類的 classification,我們可以使用 Softmax 作為最後一層的 activation function
- 我們使用 作為 classification 的種類數目
- 最後一層計算出 Z :
- 對 向量的每一個 使用 softmax activation function
- 所有的 加起來要等於 1
- 用實際例子舉例
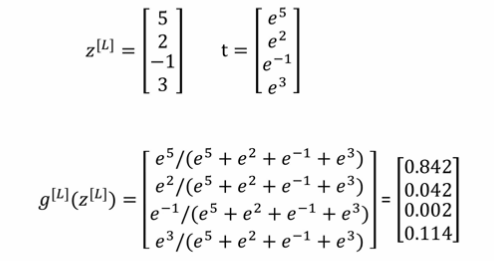
Softmax Cost Function
- Loss function :
- 在 vector 中因為只有第 i 個 entry 為 1
- 所以其他都等於 0
- 所以 Loss function 可以簡化成
- 也就是要讓 越大,cost 才會越接近 0
- 於是 Cost Function 等於
Softmax Gradient Descent
- Softmax regression 在回推 backpropogation 時的算法跟 logistic 時一模一樣
- 只是以向量模式取代實數
Deep Learning Frameworks
- 現在有非常多種框架能夠簡單應用 deep learning
- Caffe / Caffe 2
- CNTK
- DL4J
- Keras
- Lasagne
- mxnet
- PaddlePaddle
- TensorFlow
- Theano
- Torch
- 但選擇時最好基於以下幾個重點
- 方便編寫程式
- 運行速度要快 (特別是大型數據)
- 是否真正開放 (不但是開源、而且需要良好管理、能夠持續更新)