Optimization algorithms

本文介紹了有助於進行深度學習最佳化的算法，包括 Mini-Batch Gradient Descent 以及 Exponentially Weighted Averages。因為 Batch Gradient Descent 對整個 training set 進行一次 gradient descent，每個 iteration 時間較長，訓練過程較慢。Mini-Batch 將 Batch 和 Stochastic Gradient Descent 優點合併，但需要找出適合的 batch size。Exponentially Weighted Averages 是一個用於分析移動平均的算法，可以減緩短期波動，反映長期趨勢。

另外本文還介紹了一些優化 Gradient Descent 的算法，包括 Momentum、RMSprop 和 Adam，並介紹了如何應用學習率衰減的技術，以及深度學習中的局部極值和鞍點問題。

Mini-Batch Gradient Descent

• 當 training set 非常大，例如有 m = 5000000 筆時
  • Batch gradient descent 需要跑完所有 m 才能進行一次下降
• Mini-batch gradient descent 從 m 中取出一批一批 training set
  • 假設每 1000 筆一批
  • 那就可以執行 5000 次下降
    • 全部 5000 筆執行完一次，稱為 1 epoch
  • 前 1000 筆用 $(X^{\{1\}}, Y^{\{1\}})$ 表示，
  • 最後 1000 筆就是 $(X^{\{5000\}}, Y^{\{5000\}})$
  • 每次執行的 gradient descent 和 batch 時一模一樣
  • 執行 5000 次完還可以重複進行，直到 converge
    • 執行多次 epoch
• Batch 和 Mini-Batch 的 cost per iteration 如下

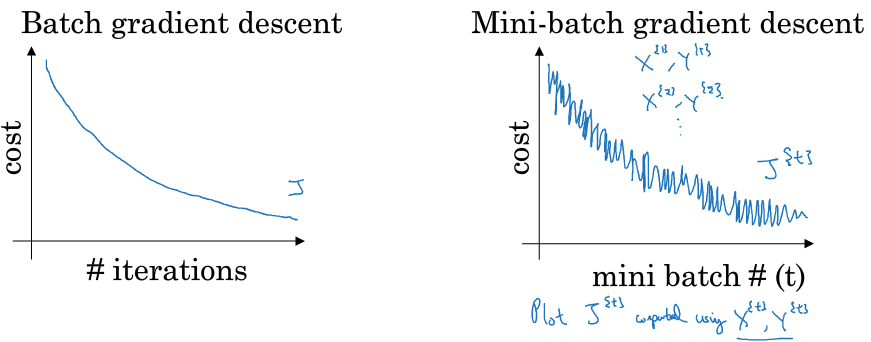Batch vs Mini-Batch

Mini-Batch Size

• Mini-batch size 也是一個需要經驗的 hyperparameter
• 當 size = m 時
  • 就是原本的 Batch gradient descent
• 當 size = 1 時
  • 稱為 Stochastic gradient descent
  • 每讀一筆 training set 就做一次 gradient descent

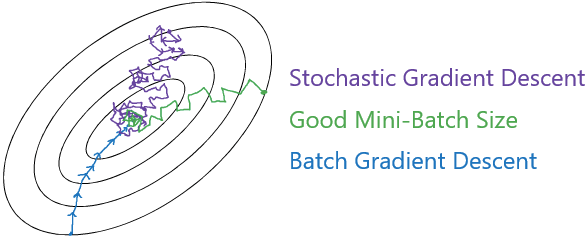Batch size comparison

• Batch Gradient Descent
  • 對整個 m 進行一次 gradient descent
  • 下降幅度較大，很穩定往最小值移動
  • 每個 iteration 時間很長，訓練過程很慢
• Stochastic Gradient Descent
  • 速度很快
  • 但完全沒享受到 vectorization 的加速優勢
  • 永遠不會 converge，會在最小值周圍移動
    • 可以用 learning rate decay 解決
• Mini-Batch
  • 將兩者優點合併，但需要找出適合的 batch size
  • 若 m 較小，如 $m \le 2000$ 可以考慮直接使用 batch gradient descent
  • 若 m 較大，通常使用 $2^6, 2^7, 2^8, 2^9$ 作為 batch size 較好
    • 符合電腦 memory 儲存方式
    • 另外，size 一定要定義為 CPU/GPU 裝的下的大小

Exponentially Weighted Averages

• 在實作一些比 gradient descent 還要棒的 optimization algorithm 前
• 需要先學會使用 Exponentially Weighted Averages
• 這是一種用於分析移動平均的算法、像天氣、股票等一連串資訊
  • 要試著減緩短期波動、反映長期趨勢

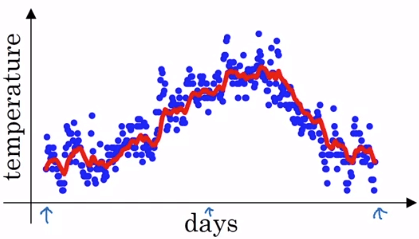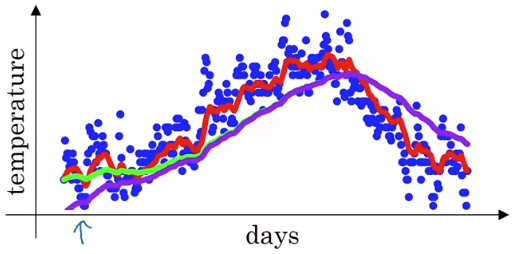
Exponentially Weighted Averages

• 例如上圖是倫敦一整年的溫度變化圖
• 我們想算出他的移動平均 (紅線)
• 我們定義 $v_i$ 為前一天算完的平均 ($v_0 = 0$)
• 定義 $\theta_i$ 為每一天的溫度
• 我們可以用以下算法算出紅線

$$\begin{aligned} v_0 &= 0 \\ v_1 &= 0.9 v_0 + 0.1\theta_1 \\ v_2 &= 0.9 v_1 + 0.1\theta_2 \\ \vdots \\ v_{365} &= 0.9 v_{364} + 0.1\theta_{365} \end{aligned}$$

• 可以將以上循環定義為一個簡單公式
  • 把 $v_t$ 想成是 $\approx \frac{1}{1-\beta}$ 天的溫度

$$v_t = \beta v_{t-1} + (1-\beta) \theta_t$$

• 所以 $\beta$ 是一個 weight，在上面例子是 0.9
  • 代表每次得到的 $v$ 是平均前 10 天的溫度
• 若設定 $\beta = 0.98$
  • 每次得到的 $v$ 就是平均前 50 天的溫度
• 設定 $\beta = 0.5$
  • 得到 $v$ 為平均前 2 天的溫度
• 所以 $\beta$ 越小，代表平均越少前面天數，就會改變的越激烈
  • 所以綠線就是平均前 50 天所產生的線 ($\beta = 0.98$)
  • 黃線則是平均前 2 天 ($\beta = 0.5$)
• 我們這目標是在不同分析中找到類似紅色的線

Exponentially Weighted Averages

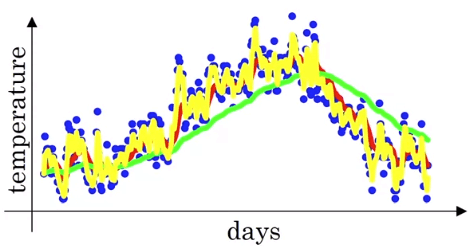Understanding Exponentially Weighted Averages

• 我們設定 $\beta = 0.9$，可以計算出

$$\begin{aligned} \vdots& \\ v_{98} &= 0.9v_{97} + 0.1\theta_{98} \\ v_{99} &= 0.9v_{98} + 0.1\theta_{99} \\ v_{100} &= 0.9v_{99} + 0.1\theta_{100} \end{aligned}$$

• 然後把計算到 $v_{100}$ 的值攤開

$$\begin{aligned} v_{100} &= 0.1\theta_{100} + 0.1 \times 0.9\theta_{99} + 0.9v_{98} \\ &= 0.1\theta_{100} + 0.1 \times 0.9\theta_{99} + 0.1 \times 0.9^2\theta_{98} + 0.9v_{97} \\ &= \cdots \end{aligned}$$

• 因為每個 $\theta_i$ 代表第 i 天的真實溫度
• 每個 $\theta_i$ 前方的 $0.1 \times 0.9^{(n-i)}$ 稱為 Bias correction
  • 所有的 Bias correction 加總會接近或等於 1
• 而真實溫度會隨著 Bias correction 不斷被降低 (被無視)

$$\lim_{\beta\rightarrow 0}(1-\beta)^{\frac{1}{\beta}} = \frac{1}{e} \approx 0.368$$

• 上面這個公式代表當 $\beta = 0.9$ 時

  • 10 天後的溫度在乘上 bias correction 後，已經下降到原本的 1/3 左右
  • 所以越往後的溫度根本等於沒有用一樣

• 最後，在計算 exponentially weighted averages 只需要一行程式碼

  • 並且只需要一個儲存 v 的 memory 位置
  • 因為不需定義所有的 v，只需對同一個 v 進行運算更新即可

$$\begin{aligned} \text{Repeat : }&\\ &v := \beta v + (1-\beta) \theta_t \end{aligned}$$

• 雖然不會比你直接計算前 10 天、50 天的平均還要精準
• 但他只需要一行代碼、而且佔用非常少 memory、效率極高

Bias Correction Adjustment

Bias Correction Adjustment

• 實際上會因為 $v_t$ 從 0 開始
• 所以 $v_1 = \beta v_0 + (1-\beta)\theta_1$
• 前項完全被消掉，因此第一個 v 僅為當天溫度的 ($1-\beta$) 倍
• 會產生紫色線一樣慢熱的狀況
• 我們可以修改 $v_t$ 為以下公式

$$v_t = \frac{\beta v_{t-1} + (1-\beta)\theta_t}{1-\beta^t}$$

• 這個修正讓 $v$ 在一開始可以正常一點
• 而隨著 $t$ 越大，$\beta^t$ 將趨近於 0，代表整個修正不再影響結果

Gradient Descent with Momentum

• Momentum 事實上就是對 gradient 進行 Exponentially weighted averages 的計算
  • 並用新產生的 gradient 來更新下降

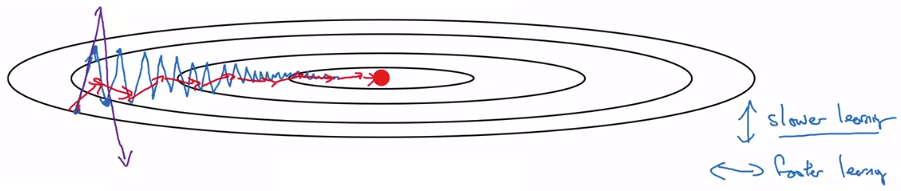Gradient Descent with Momentum

• 上面用一個 intuition 解釋
• 藍線為一般的 gradient descent
  • 有一些不往最小值移動的 oscillation
• 紫線為 learning rate $\alpha$ 特別大的 gradient descent
  • oscillation 更大，甚至會 overshoot
• 我們的目的就是要減少上下擺動的幅度
  • 並且維持甚至增加往最小值移動的幅度
  • 紅線的部分
• 所以 gradient descent with momentum 的實作如下

$$\begin{aligned} \text{On iteration t :}&\\ &\text{Compute } dw, db \text{ on current mini-batch} \\ & v_{dW} = \beta (v_{dW}) + (1-\beta) dW \\ & v_{db} = \beta (v_{db}) + (1-\beta) db \\ &W = W - \alpha (v_{dW}) \\ &b = b - \alpha (v_{db}) \end{aligned}$$

• 其中 $v_{dW}, v_{db}$ 就是計算 exponentially weighted averages 的方法
• 而 $\beta$ 跟 $\alpha$ 一樣，是一個 hyperparameter
  • 當 $\beta = 0$，就等於一般的 gradient descent
  • 通常會設置 $\beta = 0.9$，會很好的得到紅線的效果
• momentum 不需要修正 bias correction
  • 因為通常移動十次左右，就已經是不錯的移動平均

RMSprop

• RMSprop 全名為 Root-Mean-Square Propagation
• 我們假設 $w$ 和 $b$ 是主要影響 oscillation 的 parameters
  • 而 $b$ 是影響上下擺動較嚴重的 parameter

RMSprop

• 我們先來計算 RMSprop
• 為了跟 momentum 區分，RMSprop 中的 $\beta$ 改為 $\beta_2$

$$\begin{aligned} \text{On iteration t :}&\\ &\text{Compute } dw, db \text{ on current mini-batch} \\ & s_{dW} = \beta_2 (s_{dW}) + (1-\beta_2) (dW)^2 \\ & s_{db} = \beta_2 (s_{db}) + (1-\beta_2) (db)^2 \\ &W = W - \alpha \frac{dw}{\sqrt{s_{dW} + \epsilon}} \\ &b = b - \alpha \frac{db}{\sqrt{s_{db} + \epsilon}} \end{aligned}$$

• 因為 $W$ 較小，所以用 $(dW)^2$ 計算的 $s_{dW}$ 也會較小
  • 那麼更新 $W$ 時，$s_{dW}$ 在分母，算出來的 $dw$ 就適中
• 而 $b$ 較大，所以用 $(db)^2$ 計算的 $s_{db}$ 就會較大
  • 那麼更新 $b$ 時，$s_{db}$ 在分母較大，算出來的 $db$ 就會變小
  • 就可以抑制上下的 osciilation
• 另外在分母加上 $\epsilon$，是為了防止分母太小，導致數值不穩定
  • $\epsilon$ 通常為 10e-8
• 這裡只是舉 $b$ 為影響上下擺動嚴重的 parameter
  • 實際例子可能為 $w_1, w_2, w_3, \cdots$ 是影響上下擺動的原因
  • 而 $w_4, w_5, \cdots$ 是不影響的
• $\beta_2$ 也是一個 hyperparameter

Adam

• Adam 的全名為 Adaptive Moment Estimation
• Adam 將 momentum 和 RMSprop 融合在一起，得到更好效果
• 以下是 Adam 算法

1. 初始化以下參數 $v_{dW} = 0, v_{db} = 0, s_{dW} = 0, s_{db} = 0$
2. 在每個 iteration t 進行計算
   • 在 momentum 部分的 $\beta$ 用 $\beta_1$ 表示
   • 在 RMSprop 部分的 $\beta$ 用 $\beta_2$ 表示

$$\begin{aligned} &\text{Compute } dw, db \text{ on current mini-batch} \\ &v_{dW} = \beta_1 (v_{dW}) + (1-\beta_1) dW \\ &v_{db} = \beta_1 (v_{db}) + (1-\beta_1) db \\ &s_{dW} = \beta_2 (s_{dW}) + (1-\beta_2) (dW)^2 \\ &s_{db} = \beta_2 (s_{db}) + (1-\beta_2) (db)^2 \end{aligned}$$

3. 接著在 Adam，要對這四個參數進行 bias correction adjustment

$$\begin{aligned} v_{dW}^{\text{corrected}} &= \frac{v_{dW}}{1-\beta_1^t} \\ v_{db}^{\text{corrected}} &= \frac{v_{db}}{1-\beta_1^t} \\ s_{dW}^{\text{corrected}} &= \frac{s_{dW}}{1-\beta_2^t} \\ s_{db}^{\text{corrected}} &= \frac{s_{db}}{1-\beta_2^t} \end{aligned}$$

4. 最終更新參數 $w, b$

$$\begin{aligned} W &= W - \alpha \frac{v_{dW}^{\text{corrected}}}{\sqrt{s_{dW}^{\text{corrected}} + \epsilon}} \\ b &= b - \alpha \frac{v_{db}^{\text{corrected}}}{\sqrt{s_{db}^{\text{corrected}} + \epsilon}} \end{aligned}$$

Hyperparameter choices

• 以上就是整個 Adam 算法
• 在這個算法中出現非常多 hyperparameters
  • 要怎麼設置以下一一介紹
• $\alpha$ : learning rate，需要自己慢慢找到一個合適的
• $\beta_1$ : momentum 使用到的像 exponentially weighted averages 的 weight
  • 常用的設定為 0.9
• $\beta_2$ : RMSprop 所使用到的 $\beta$，一樣是由 exponentially weighted averages 而來
  • Adam 作者建議設定為 0.999
• $\epsilon$ : 不重要，用預設的 10e-8 即可
• $\beta_1, \beta_2, \epsilon$ 通常不太需要去修改調整

Learning Rate Decay

• 若使用固定 $\alpha$ 的 mini-batch，那麼 gradient descent 幾乎不會準確 converge
  • gradient descent 將會在最小值周圍擺動
• 為此我們可以讓 $\alpha$ 隨著時間慢慢減少
  • 一開始 $\alpha$ 較大，幫助我們跨大步伐
  • 最終 $\alpha$ 變小，幫助我們在最小值收斂
• 最常用的 learning rate decay 公式如下
  $$\alpha = \frac{1}{1 + \text{decay-rate} \times \text{epoch-num}} \times \alpha_0$$
  • $\alpha_0$ 是初始的 learning rate
  • k epoch 代表所有 mini-batch 全跑過 k 遍
  • decay-rate 是一個 hyperparameter
• 假設我們設計 $\alpha_0 = 0.2, \text{decay-rate = 1}$
  • 那 $\alpha$ 將會隨著跑過所有 mini-batch 的次數而下降

Epoch	$\alpha$
1	0.1
2	0.067
3	0.05
4	0.04
...	...

Other Learning Rate Decay Formula

• Exponentially Decay
• $\alpha = 0.95^{\text{epoch-num}}\times\alpha_0$
• $\alpha = \frac{\text{constant}}{\sqrt{\text{epoch-num}}}\times\alpha_0$
• $\alpha = \frac{\text{constant}}{\sqrt{\text{mini-batch-num t}}}\times\alpha_0$
• Discrete staircase
• Manual decay : Only small num training set

Problem of Local Optima

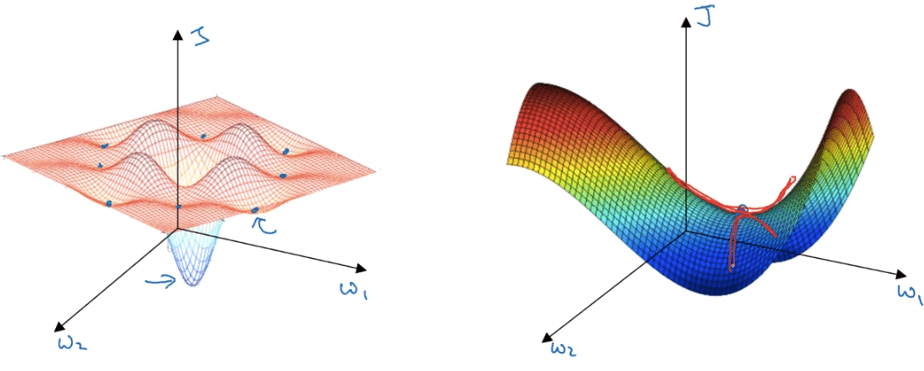
• 在 machine learning 時，我們對梯度接近 0 的想像都是 local optima
  • 圖面上很多凹點，然後你隨便掉進一個凹點就出不來
• 但在 deep learning 中，你的維度變的非常大
  • 通常會遇到梯度接近 0 的地方是 saddle point
  • 所以在大型的 nn、有著大量參數、較高維度時
    • 困在 local optima 的情況是不太可能的
• 所以 deep learning optimization 的問題不是 local optima 而是 plateaus
  • 這個 saddle point 或者 plateaus 會使得 learning 速度變慢
  • 所以才會不斷的推出新的 optimization algorithm
    • Momentum, RMSprop, Adam, ...
    • 這些算法能夠加速離開這些梯度接近 0 的點
    • 甚至找出更棒的 optimization algorithm 是 deep learning 的挑戰之一

Local Optima and Saddle Point