Regularizing Neural Network

Regularization 是 machine learning 中常見的技術，用於限制模型參數和權重，以減少模型對訓練數據過度擬合的可能性。而當我們將其套用到 Neural Network 上時，也有 Frobenius Norm 以及 Weight Decay 等技術可以做到 regularization。此外，我們也會使用 Dropout Regularization 來避免 Overfitting，而 Data Augmentation 和 Early Stopping 也是可以用來避免 Overfitting 的方法。本文將會詳細解釋這些技術，以及它們彼此之間的關係。

Regularization

我們在 machine learning 中也有提到的 regularization
我們重新提出，並且將他應用到 neural network 中
這是 logistic regression $J(\theta)$ 使用 regularization
- $J(w, b) = \frac{1}{m}\sum_{i=1}^m\mathcal{L}(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m}\lVert w\rVert^2_2$
後面加的這一項 regularization 可以細分為 L2 和 L1 regularization
- L2 就是上面寫的
  - $\frac{\lambda}{2m}\lVert w\rVert^2_2 = \frac{\lambda}{2m}\sum_{j=1}^{n_x}w_j^2 = \frac{\lambda}{2m} w^Tw$
- L1 就是沒有平方的版本
  - $\frac{\lambda}{2m}\lVert w\rVert_1 = \frac{\lambda}{2m}\sum_{j=1}^{n_x}\lvert w_j\rvert$
- 因為 L1 會產生 sparse matrix (很多 entries 為 0)
- 所以通常大家都使用 L2

Regularization in Neural Network

在 nn 中所用到的 L2 regularization 稱為 Frobenius Norm (F 底標記)
- 也就是整個 $w (n^{[l-1]}, n^{[l]})$ 每個 entries 的平方和
- $\lVert w^{[l]}\rVert_F^2 = \sum_{i=1}^{n^{[l-1]}}\sum_{j=1}^{n^{[l]}}(w^{[l]}_{ij})^2$
所以整個包含 regularization 的 neural network cost 為
- $J(w^{[1]},b^{[1],\cdots,w^{[L]},b^{[L]}}) = \frac{1}{m}\mathcal{L}(\hat{y}^{(i)},y^{(i)}) + \frac{\lambda}{2m}\sum_{l=1}^L \lVert w^{[l]}\rVert_F^2$

Weight decay

另外，當 L2 套用之後，會讓 gradient descent 在每次更新時， $W$ 都會乘以一個小於 1 的數
所以 L2 又稱為 weight decay

\begin{aligned} dW^{[l]} &= \frac{\partial \mathcal{L}}{\partial w^{[l]}} + \frac{\lambda}{m}W^{[l]} \\ &\text{insert into gradient descent} \\ W^{[l]} &:= W^{[l]} - \alpha dW^{[l]}\\ &:= W^{[l]} - \alpha\begin{bmatrix}\frac{\partial \mathcal{L}}{\partial w^{[l]}} + \frac{\lambda}{m}W^{[l]}\end{bmatrix}\\ &:= W^{[l]} - \alpha\frac{\lambda}{m}W^{[l]} - \alpha\frac{\partial \mathcal{L}}{\partial w^{[l]}} \\ &:= (1-\frac{\partial\lambda}{m})W^{[l]} - \alpha\frac{\partial \mathcal{L}}{\partial w^{[l]}} \end{aligned}

Regularization Intuition

這裡講解的 regularization 原因和 machine learning 裡類似
但是是以 nn 為基底來解釋

Intuition 1

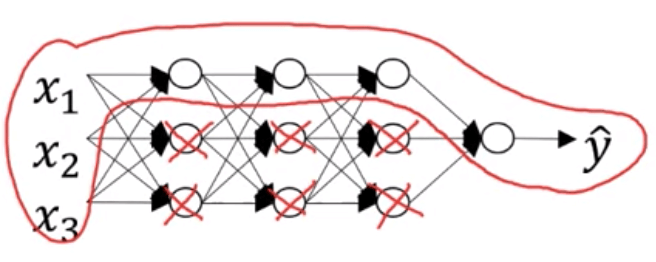
在 regularization 中 $\lambda$ 增加
parameters $W$ 中一些不重要的 unit 就會被降低 $\approx 0$
這就像把一些 neuron 從 nn 中去除掉，變成一個較小的 nn
進而避免 overfitting

Intuition 2

假設 activation function 為 tanh
Regularization 將 $\lambda$ 上升
所以 $W^{[l]}$ 就會下降
進而影響 $z^{[l]} = w^{[l]}a^{[l-1]}+b^{[l]}$ 變小
降低 $z^{[l]}$ 我們就會得到 unit 的值介於上圖中間紅色 linear 區域
此時 tanh(z) 會接近 linear function
整個網路就會近似 linear nn 一樣，不會 overfitting

Dropout Regularization

Dropout 對每一個 hidden layer 設定一個隨機消除 neuron 的機率
會讓每次訓練的 nn 變成一個較小的 nn
Dropout 通常使用於 Computer vision

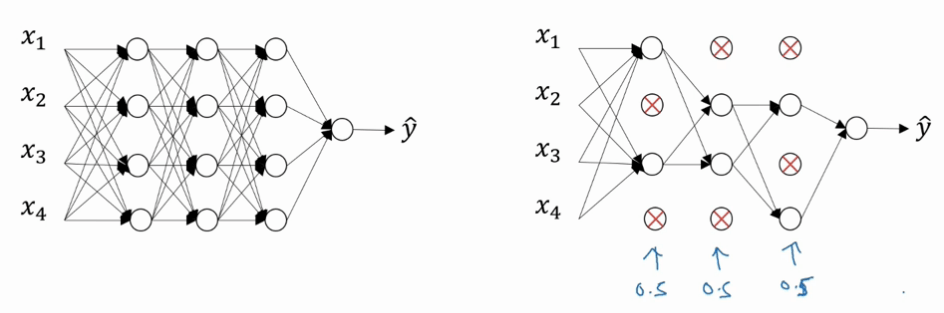
通常會使用 Inverted dropout 來 implement dropout
以下是對第 l 層進行 dropout 的過程

keep_prob = 0.8  # hold neuron probability
dl = np.random.rand(al.shape[0], al.shape[1]) < keep_prob
al = np.multiply(al, dl)
al /= keep_prob

有點類似遮罩的感覺，將 al 乘以 0/1 遮罩 dl
最後 al /= keep_prob 就是 inverted dropout 的精神
- 是為了避免下一層計算發生錯誤
- 因為 al 有些 neuron 被歸零
- 所以我們在沒被歸零的 neuron 上補回 20% 期望值
另外，別在 test 時使用 dropout，會讓預測結果隨機化

Dropout Intuition

因為一個 neuron 會接收多個 features 並分配 weights 給他們，然後計算後輸出
但現在任何一個 features 都有可能消失
所以這個 neuron 在 weights 上會更平均的分配
這就類似 L2 在 shrink weights 的做法

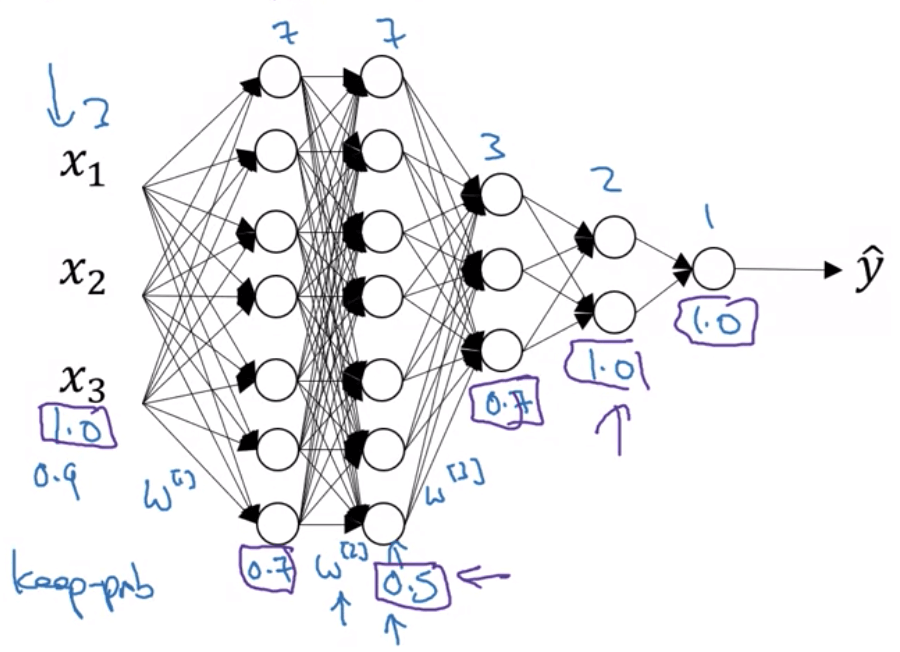
對於不同的 layer 設定的 keep_prob 也不同
通常較少 hidden units 的 layer 的 keep_prob = 1
- Input layer 通常也為 1
越多 features (weights 越大) 的 layer 的 keep_prob 越小越好
Dropout 有一個大缺點
- 就是無法正確定義出 $J(\theta)$
- 所以無法邊訓練邊看 cost function 是否正確遞減
- 通常需要將 keep_prob 先全部設定回 1 再觀察

Other regularization methods

Data Augmentation

Overfitting 往往可以依靠增加 data 數量來緩解
利用修改圖片 (flip, stretch, crop, ...)，來產生更多新的 data

Early Stopping

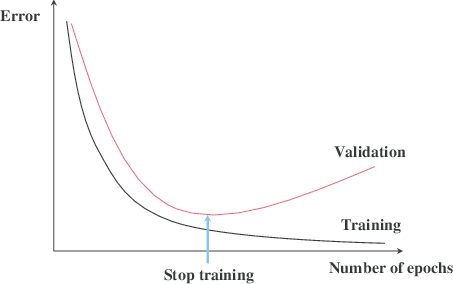
我們將 train error 和 dev error 同時 plot 在一起
當 train error 持續下降而 dev error 卻上升時
- 就是 overfitting 的開始
所以我們在此時停止 iteration，並返回 dev error 在最小時的參數
好處是不需要嘗試大量 L2 regularization
但 early stopping 有一大缺點
- 他違反了 orthogonalization

Orthogonalization

在處理一個 nn 時，我們偏向專注於一次一件事情上
第一件事是 optimize cost function
- 會用 gradient descent 等方式處理
第二件事是 not overfitting
- 會用 regularization 等方式處理
但 early stopping 既不跑完 optimization 還要時刻注意 overfitting 問題
- 將兩件事情耦合在一起

Regularization​

Regularization in Neural Network​

Weight decay​

Regularization Intuition​

Intuition 1​

Intuition 2​

Dropout Regularization​

Dropout Intuition​

Other regularization methods​

Data Augmentation​

Early Stopping​

Orthogonalization​