跳至主要内容

Setting up Optimization

在本篇文章中，我們將學習關於如何優化 cost function，也就是 gradient descent 方法。我們將學習到 normalize inputs、vanishing / exploding gradient 以及 weight initialization 等方法，以及 gradient checking 的技巧來確保訓練正確性。

Normalize Inputs​

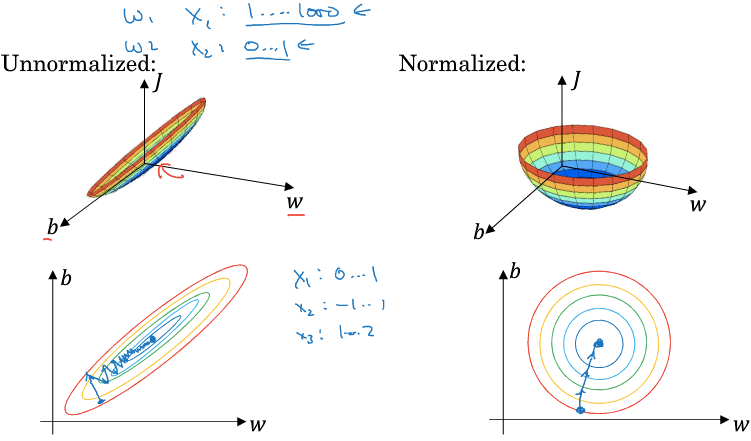
Normalize feature
Normalize feature
  • 若某個 feature xx 的 input range 非常大 (size=1 ... 1000000)
  • 那他的 cost function 會像橢圓一樣的形狀
    • 在 gradient descent 時非常緩慢曲折
  • 所以我們可以 normalize feature xx
  • 使得 cost function 變成像正常的碗狀一樣
    • 適合 implement gradient descent
  • Normalize 方法如下
  • x=x−μσx = \frac{x-\mu}{\sigma}
    • 其中的 μ\mu 是平均數 (mean)
      • μ=1m∑i=1mx(i)\mu = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}
    • 另一個 σ\sigma 是變異數 (variance)
      • σ=1m∑i=1mx(i)2\sigma = \sqrt{\frac{1}{m}\sum_{i=1}^{m}x^{(i)^2}}

Vanishing / Exploding Gradient​

  • 在 gradient 有可能出現 vanishing gradient 或是 exploding gradient 的問題
    • 梯度消失、梯度爆炸
  • 通常發生在 nn 有非常多 layers 時
  • 可被視為阻檔 deep learning 發展的一個原因
  • 也就是 weights 將 decrease / increase exponentially
  • 假設 activation function 是一個 linear function g(z)=zg(z) = z
  • 假設所有的 b[l]=0b^{[l]} = 0
  • 如此一來，y^\hat{y} 可以很容易的算出
y^=W[L]W[L−1]⋯W[2]W[1]X\hat{y} = W^{[L]}W^{[L-1]}\cdots W^{[2]}W^{[1]}X
  • 若所有 W[l]W^{[l]} 的值大於 1 時，weights 將會 increase exponentially
  • 若所有 W[l]W^{[l]} 的值小於 1 時，weights 將會 decrease exponentially
  • 對於 backpropogation 的導數一模一樣
  • 這會讓訓練難度變得非常高

Weight Initialization​

  • Weight initialization 雖然沒辦法完全解決 vanishing / exploding gradient
    • 但可以減緩兩者的發生
  • 從 single neuron 看起，若一個 neuron 得到很多個 input，那麼計算 z 等於
z=w1x1+w2x2+⋯wnxn+bz = w_1x_1 + w_2x_2 +\cdots w_nx_n + b
  • 因為 n 很大，所以我們勢必要讓每個 wiw_i 都越小越好
  • 為此，我們套用一招 Xavier initialization Var(wi)=1/n\text{Var}(w_i) = 1/n
    • 用 python 寫成
    WL = np.random.randn(WL.shape[0], WL.shape[1]) * np.sqrt(1/n)
    • 其中 n 是输入的神经元个数，即 WL.shape[1]
  • 若是 activation function 使用 ReLU 時
    • 可以套用另一招 He initialization Var(wi)=2/n\text{Var}(w_i) = 2/n

Gradient Checking​

  • Gradient Checking 可以用來檢查 backpropogation 的導數是否正確
  • 先利用雙邊誤差方式計算出近似於 slope 的值
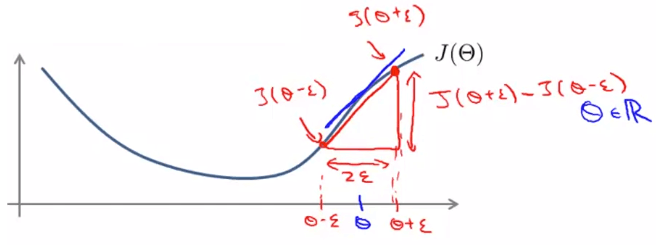
Gradient checking
Gradient checking
J′(θ)=J(θ+ϵ)−J(θ−ϵ)2ϵJ'(\theta) = \frac{J(\theta+\epsilon) - J(\theta-\epsilon)}{2\epsilon}
  • 當有多個 parameters 時，我們會針對每一個 parameter 都做一次雙邊誤差計算
For each i:dθapprox[i]=J(θ1,θ2,⋯ ,θi+ϵ,⋯ )−J(θ1,θ2,⋯ ,θi−ϵ,⋯ )2ϵ\begin{aligned} \text{For each i} &: \\ &d\theta_\text{approx}[i] = \frac{J(\theta_1,\theta_2,\cdots,\theta_i+\epsilon, \cdots) - J(\theta_1,\theta_2,\cdots,\theta_i-\epsilon, \cdots)}{2\epsilon} \end{aligned}
  • 我們希望每一個算出來的值，都可以跟自己計算的一樣
  • dθapprox[i]≈dθ[i]=∂J∂θid\theta_\text{approx}[i] \approx d\theta[i] = \frac{\partial J}{\partial \theta_i}
  • 我們用以下方式來 check，可以固定比例，不怕數值過小
∥dθapprox−dθ∥2∥dθapprox∥2+∥dθ∥2\frac{\lVert d\theta_\text{approx} - d\theta \rVert_2}{\lVert d\theta_\text{approx}\rVert_2 + \lVert d\theta \rVert_2}
  • 若結果和 ϵ\epsilon 近似，表示 backpropogation 做得不錯
  • 另外上面計算時用到的為 Euclidean norm
    • ∥x∥2=∑i=1N∣xi∣2\lVert x\rVert_2 = \sum_{i=1}^N\lvert x_i\rvert^2

Summary​

  • Gradient checking 只適用於 debug，training 時應該關掉
  • Fail 時，可以去觀察每一個 θ\theta 來找出 bug
  • 記得要包含 regularization
  • Gradient checking 不適合跟 dropout regularization 一起使用