Advice for Applying ML

在機器學習中，評估學習演算法是非常重要的一個步驟。我們需要透過調整模型參數，和適當的測試方法來確保模型表現的穩定性。本文將介紹幾個常見的模型評估方法，以及對於避免 overfitting 的方法，例如 regularization 和 cross validation。

Evaluating a Learning Algorithm

Debugging learning algorithm

當你的 Cost function 怎麼算都不對時，下一步該怎麼做 ?

• 找更多 training examples
• 減少 features
• 增加 features
• 試著加入 polynomial features
• Increasing $\lambda$
• Decreasing $\lambda$

如果只是隨便從中任選一個當解方，那可能會花上數個月解決

所以我們必須要採取 Machine Learning Diagnostic

Diagnostic 可能會發非常多時間 implement

但他可以給我們 guidance 以及 insight of learning algorithm

Evaluating a Hypothesis

為了避免 hypothesis overfitting

我們也將 training examples 拆成兩組，其中

70% 作為 training set，而 30% 作為 test set (拆分時最好是隨機的狀態)

所以現在 learning 的順序變成 :

1. 找出能夠 minimize $J_\text{train}(\Theta)$ 的 $\Theta$ 得到 hypothesis
2. 計算對應的 test set error $J_\text{test}(\Theta)$

在 Linear regression 中，我們表示 test set error 為 :

$$J_\text{test}(\Theta) = \frac{1}{2m_\text{test}}\sum_{i=1}^{m_\text{test}}(h_\Theta(x_\text{test}^{(i)}) - y_\text{test}^{(i)})$$

在 Logistic regression 中，我們重新定義了 Misclassification error (0/1 misclassification error)

$$\begin{aligned} err(h_\Theta(x), y) = \left\{\begin{matrix} &1 && \text{if }h_\Theta(x) \ge 0.5 \text{ and } y = 0 \text{ || } h_\Theta(x) < 0.5 \text{ and } y = 1 \\ &0 &&\text{otherwise} \end{matrix}\right. \end{aligned}$$

而 Average test error 即告訴我們有多少的 test set 被 misclassified :

$$\text{Test Error } = \frac{1}{m_\text{test}}\sum_{i=1}^{m_\text{test}} err(h_\Theta(x_\text{test}^{(i)}), y_\text{test}^{(i)})$$

Model Selection

為了進一步解決 Overfitting 的問題，我們能夠採用 model selection 的辦法

一次列出不同 degree 的多種 model 來測試

首先對各個 model 計算出 $\theta$

然後把每個 $\theta$ 都丟進 $J_\text{test}(\theta)$ 測試，找出最小的 model

$$\begin{aligned} &d=1, &&h_\theta(x) = \theta_0 + \theta_1x&&\rightarrow \theta^{(1)}\rightarrow J_\text{test}(\theta^{(1)})\\ &d=2, &&h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2&&\rightarrow \theta^{(2)}\rightarrow J_\text{test}(\theta^{(2)})\\ &&\vdots\\ &d=10, &&h_\theta(x) = \theta_0 + \theta_1x + \cdots + \theta_{10}x^{10}&&\rightarrow \theta^{(10)}\rightarrow J_\text{test}(\theta^{(10)}) \end{aligned}$$

但我們提早用了 test set 當作測試 model 的 data

難道我們又要再用 test set 進行最終測試嗎 ?

Cross Validation (CV) Set

為此我們將資料拆成三等分

多了一種 validation set 用來當作 model selection 的 data

• Training set : 60%
• Validation set : 20%
• Test set : 20%

現在我們將進行三個步驟，各別算出 train, cv, test 的 error values :

1. 利用 training set 找出每個 degree model 的最佳 $\theta$
2. 利用 validation set 找出最小 error 的 degree model
3. 將找到的 model 與 test set 作 $J_\text{test}(\theta^{(d)})$ 的最終測試
   • d = theta from polynomial with lower error

這麼一來，就不會再發生 test set 偷看的問題了 !

Bias vs. Variance

為了認清每一個 degree 是 underfit 或是 overfit

我們需要先知道 bias 和 variance 是什麼

Bias and variance

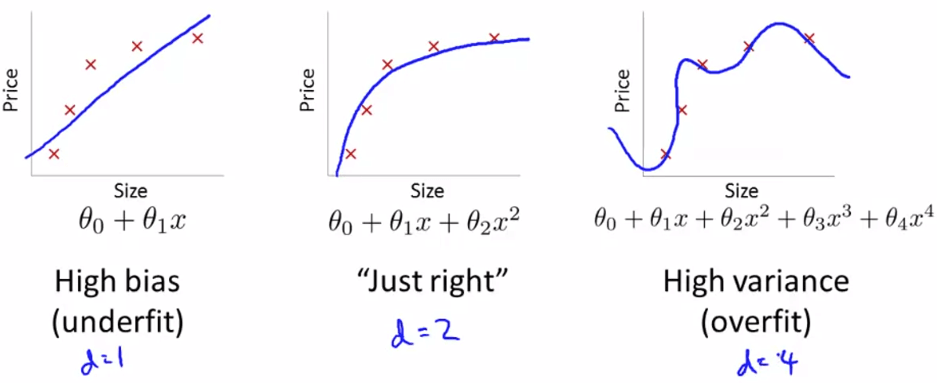
其實 high bias 就是指 underfit，而 high variance 就是 overfit

我們知道不管 overfitting，training error 會隨著 degree 增加而減少

而因為 overfitting 的關係，沒有了 training set 的

validation 及 test 的 error 則都會隨著 degree 增加而增加

• d increase
  • training error decrease
  • validation error increase
  • test error increase

High bias and variance

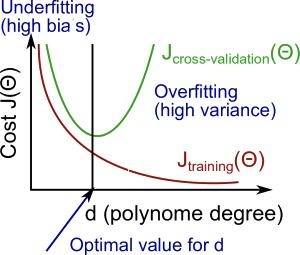
因此我們可以從這個特徵找出 cost function 是 high bias 或是 high variance

• High bias (underfit) : $J_\text{train}(\theta)$ 和 $J_\text{CV}(\theta)$ 的 error 都很高，並且 $J_\text{train}(\theta) \approx J_\text{CV}(\theta)$
• High variance (overfit) : $J_\text{train}(\theta)$ error 很低，但 $J_\text{CV}(\theta)$ 的 error 很高

Regularization with bias/variance

我們知道解決 regularization 可以解決 overfitting 的問題

但要怎麼設定 $\lambda$ ? 可不可以自動找出一個最好的 $\lambda$ ?

Lambda affect

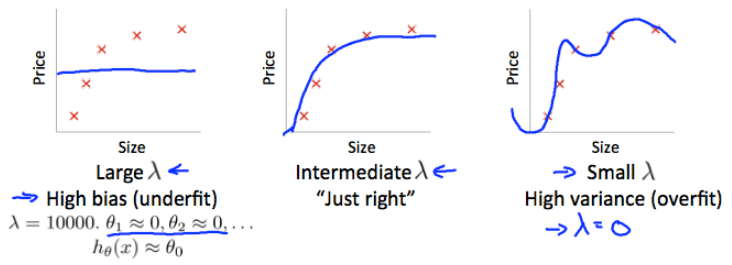
我們觀察，當 $\lambda$ 在不同程度時的變化

• $\lambda = 10000$，所有的 $\theta \approx 0$，所以變成 High bias (underfit)
• $\lambda = 0$，等於沒有 regularization，所以變成 High variance (overfit)

也就是 $\lambda$ 越小時，train cost 很低 (overfit)，但也因此 CV cost 很高

而 $\lambda$ 越大時，train cost 變高了 (underfit)，所以 CV cost 依然很高

Train and CV cost with different lambda

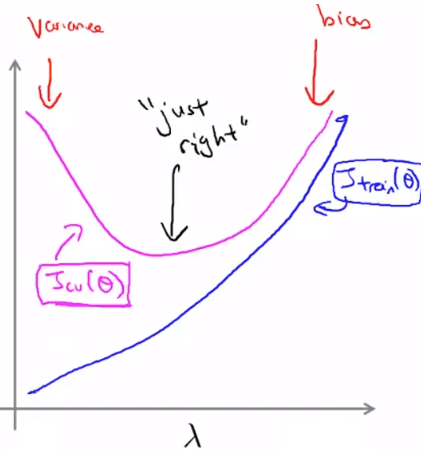
我們可以用類似 model selection 的方式來尋找 best $\lambda$

Lambda selection

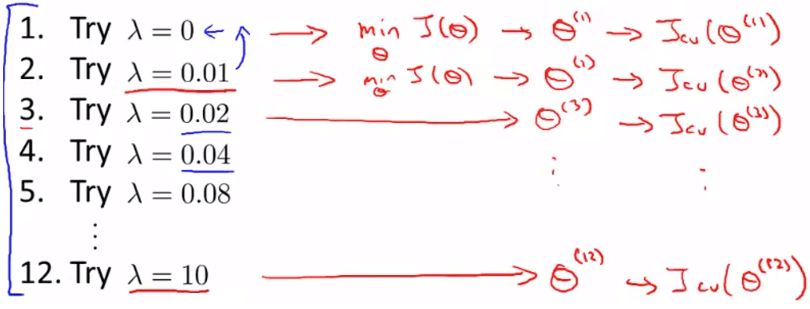
1. 首先定義一個的 $\lambda$ list (可以以 *2 列出)
2. 用每一個 $\lambda$ 去學習每一個 $\min_\theta J(\theta)$ 得到不同的 $\theta$
3. 將學到的 $\theta$ 丟到不含 regularization 的 CV cost function $J_{CV}(\theta)$ 計算
4. 找出在 CV 測試中最小 error 的 model
5. 將最好的 $\lambda \text{ and } \theta$ 丟到 $J_\text{test}(\theta)$ 測試結果

Learning Curves

現在我們可以利用一種工具來檢查 bias 或是 variance 稱作 learning curves

假設我們有一個做好的 quadratic curve 的 hypothesis

從 m = 1, 2, 3, ... 個 training sets 開始測試

一開始的 error 會非常的小，但隨著 size m 越大 error 就會變得很大

因為只有 quadratic 的 curve 很難 fit 越來越多的 data

High bias experience

High bias 代表 underfitting

• Training sets 小的時候

  • $J_\text{train}(\theta)$ 會非常小 (因為訓練過)
  • $J_\text{CV}(\theta)$ 會非常大 (因為不是訓練的 data，且只有一點點 data)

• Training sets 大的時候

  • $J_\text{train}(\theta)$ 會越來越大 (underfit 的關係)
  • $J_\text{CV}(\theta)$ 會降低，但還是會很大 (一樣是因為 underfit)

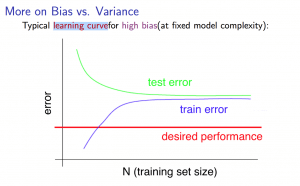
所以若 hypothesis 有 high bias problem

Learning curves 的測試結果會跟下圖差不多

• $J_\text{train}(\theta)$ 跟 $J_\text{CV}(\theta)$ 會 converge
• 但兩者都會比 desired performance 還要差

High bias curves

High variance experience

High variance 代表 overfitting

• Training sets 小的時候

  • 跟 high bias 狀況一樣
  • $J_\text{train}(\theta)$ 會非常小 (因為訓練過)
  • $J_\text{CV}(\theta)$ 會非常大 (因為不是訓練的 data，且只有一點點 data)

• Training sets 大的時候

  • $J_\text{train}(\theta)$ 會越來越大，但是好現象的越來越大
    • training size 越來越滿足 overfitting
  • $J_\text{CV}(\theta)$ 會越來越低，並且越來越接近 desired performance

High variance problem 在隨著 training sets 增加後

learning curves 會跟下圖差不多

• $J_\text{train}(\theta)$ 跟 $J_\text{CV}(\theta)$ 一樣會 converge
• 但兩者是朝著 desired performance 交會

High variance curves

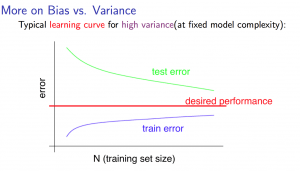
所以 High variance 問題發生時，增加 training sets size 應該是個不錯的方法

Summary

所以當你 diagnose 並發現問題點後，可以分別做正確的修正了 !

• When you get high bias problem
  • add features
  • add polynomial features $(x_1x_2, x_1^2, x_2^2, \cdots)$
  • decrease $\lambda$
• When you get high variance problem
  • add more training examples
  • try smaller sets of features
  • increase $\lambda$

Diagnose Neural Networks

• 小的 neural networks 趨向於 underfitting
  • 但他 computationally cheaper
• 大的 neural networks 趨向於 overfitting
  • 但他 computationally expensive
  • 而 overfitting 也可以透過 regularization 來修正 (increase $\lambda$)

Neural networks 預設是使用 1 hidden layer

但你也可以使用多個 hidden layer 並且搭配 cross validation sets 來訓練

Model Complexity Effects

• 當 hypothesis 的 degree 很低時
  • 會 high bias 及 low variance
  • train set 和 test set 都會 fit poorly
• 當 hypothesis 的 degree 很高時
  • 會在 train set 有 low bias 但 high variance
  • 在 train set fit perfectly
  • 但在 test set fit poorly

我們希望的 model 會介於兩者之間，fit all sets reasonably !