機器學習中,Overfitting 是一個常見的問題。當我們搜索 Hypothesis 來擬合訓練集時,可能會遇到 Underfit、Just right 和 Overfit 這三種情況。我們將 Overfitting 的定義為:太多的 features 使得求得的 Hypothesis 在 training data 上有很好的分數,但卻不能讓 test set 或真實數據使用。
要避免 Overfitting,有兩種方法:減少 features 數量,或者使用 Regularization。 Regularization 是留下所有的 features,但降低 theta 的 magnitude,這樣就不用擔心會刪除對 training 有益的 features。
為了減少多餘的 features 對 Overfitting 的影響,我們只需要將這些 features 在 cost function 中提高代價,使它們對 hypothesis 的影響降低即可。當我們將 Regularization 的公式套入 linear regression 和 logistic regression 中時,可以有效的降低 Overfitting 的影響。
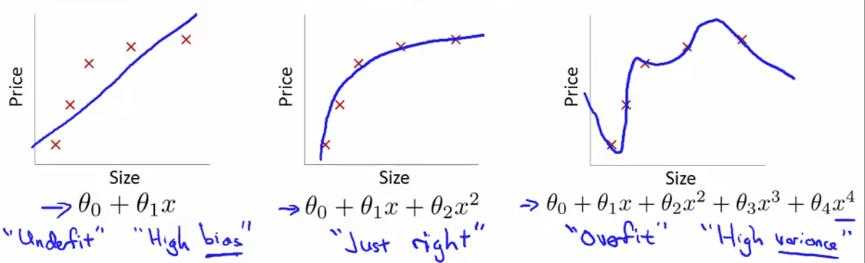
當我們要尋找 Hypothesis 來 fit 我們的 training set 時
可以遇到三種情況
Linear Regression Overfitting Underfit (High bias) Hypothesis 不是很好的 fit 這些 example data Just right Hypothesis 很好的 fit 這些 example data Overfit (High variance) Hypothesis 太過 "鑽牛角尖" 於每一個 training set 我們為 Overfitting 下一個定義 :
太多的 features,讓求得的 Hypothesis 在 training data 得到不錯分數 (cost function J 接近 0)
但完全沒辦法讓 test set 或是真實資料套入使用
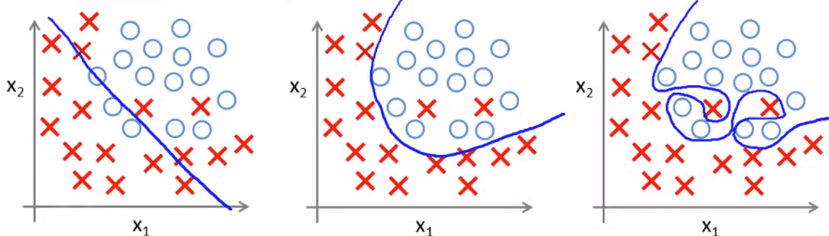
同樣的事情可以發生在 logistic regression :
Logistic Regression Overfitting 會造成 overfitting 的原因就是因為 features 使用太多了
但又不知道哪些 features 可以完全消除掉 (可能對 training 有益)
有兩種方法可以解決 :
減少 features 數量手動選擇不要的 features 使用 model selection algorithm (later in other course) Regularization留下全部 features,但降低 theta's 的 magnitude 這方法就可以不用擔心會不會刪掉對 training 有益的 features 若我們想降低多餘 (可能) 的 features 所帶來的 overfitting 影響
我們只要將這些 features 在 cost function 的代價提高,讓他們對 hypothesis 的影響下降就好
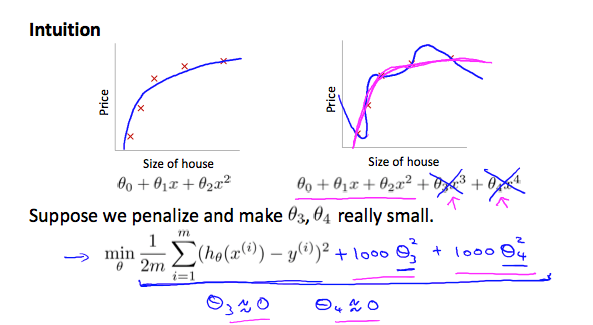
以 θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4 θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + θ 4 x 4
我們將他的 Cost function 調整為
min θ 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 \min_\theta \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 {\color{red}+1000\cdot \theta_3^2+1000\cdot\theta_4^2} θ min 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 新的 cost function 就可以在不去除 θ 3 \theta_3 θ 3 θ 4 \theta_4 θ 4
讓兩者對 hypothesis 的影響降低
1000 可以是其他較大數值,但不能夠過大
不然會使得 θ 3 \theta_3 θ 3 θ 4 \theta_4 θ 4
Regularization Intuition 右上的紫線 就是在 implement regularization 過後的新 hypothesis function
所以除了 θ 0 \theta_0 θ 0
我們將 regularization 套用到所有的 θ \theta θ
得到了新的公式 :
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^n \theta_j^2 J ( θ ) = 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ j = 1 ∑ n θ j 2 λ \lambda λ regularization parameter 將會作為 θ \theta θ 只是多了後面一個式子,就可以讓 overfitting 的影響減少 但要小心,若 λ \lambda λ 會讓每個 θ \theta θ 變回 underfit 的狀況 現在我們將 regularization 的公式套入 linear regression 和 logistic regression
先從 linear regression 的 gradient descent 開始
我們會改變所有 θ \theta θ θ 0 \theta_0 θ 0
Repeat { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] j ∈ { 1 , 2 , . . . n } } \begin{aligned} &\text{Repeat \{}\\ &\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_0^{(i)}\\ &\theta_j := \theta_j - \alpha \left[\left(\frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_j^{(i)}\right)+\frac{\lambda}{m}\theta_j\right] && j \in \begin{Bmatrix}1, 2, ... n \end{Bmatrix}\\ &\text{\}} \end{aligned} Repeat { θ 0 := θ 0 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j := θ j − α [ ( m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + m λ θ j ] } j ∈ { 1 , 2 , ... n } 我們發現第二行 θ j \theta_j θ j
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} θ j := θ j ( 1 − α m λ ) − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) 可以發現 1 − α λ m 1-\alpha\frac{\lambda}{m} 1 − α m λ
所以負號的前一項能表示每回合的 θ j \theta_j θ j
而後面一項跟原本的 gradient descent 一模一樣
要將 regularization 加入 normal equation 中
只需簡單加入 λ ⋅ L \lambda \cdot L λ ⋅ L L L L
這個矩陣為一個 ( n − 1 ) × ( n − 1 ) (n-1)\times(n-1) ( n − 1 ) × ( n − 1 )
有一個 0 的原因就是不想要變動到 θ 0 \theta_0 θ 0
θ = ( X T X + λ ⋅ [ 0 1 1 ⋱ 1 ] ) − 1 X T y \begin{aligned} \theta = \left(X^TX + \lambda \cdot \begin{bmatrix} 0 \\ & 1 \\ && 1 \\ &&& \ddots \\ &&&&1 \end{bmatrix} \right)^{-1}X^Ty \end{aligned} θ = ⎝ ⎛ X T X + λ ⋅ ⎣ ⎡ 0 1 1 ⋱ 1 ⎦ ⎤ ⎠ ⎞ − 1 X T y 將 regularization 套入 normal equation 也有另一個好處
之前說過若 features 大於 training examples 數量太多
則 X T X X^TX X T X
但現在有了 λ ⋅ L \lambda \cdot L λ ⋅ L
X T X + λ ⋅ L X^TX + \lambda \cdot L X T X + λ ⋅ L
我們一樣來將 regularization 套用在 logistic regression
讓 overfitting 的藍線變為正常的紫線 hypothesis
Regularized logistic regression 一樣在 logistic cost function
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) )) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ))] 的最後加上 regularization 的式子得到 :
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) )) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ))] + 2 m λ j = 1 ∑ n θ j 2 注意我們一樣不想變動到 θ 0 \theta_0 θ 0
所以 regularization 的 summation 從 1 開始 !
接著套進 gradient descent
Repeat { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] j ∈ { 1 , 2 , . . . n } } \begin{aligned} &\text{Repeat \{}\\ &\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_0^{(i)}\\ &\theta_j := \theta_j - \alpha \left[\left(\frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_j^{(i)}\right)+\frac{\lambda}{m}\theta_j\right] && j \in \begin{Bmatrix}1, 2, ... n \end{Bmatrix}\\ &\text{\}} \end{aligned} Repeat { θ 0 := θ 0 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j := θ j − α [ ( m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + m λ θ j ] } j ∈ { 1 , 2 , ... n } 其實跟 linear regression 一樣
只是 h θ ( x ) = 1 1 + e − θ T x h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}} h θ ( x ) = 1 + e − θ T x 1
在 Octave 實作 logistic regression 的 advanced optimization 時
這些 code 又該怎麼跟 regularization 一起實作 :
function [jVal, gradient] = costFunction(theta) jVal = [ code to compute J ( θ ) ] ; → J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 gradient(1) = [ code to compute d d θ 0 J ( θ ) ] ; → 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) gradient(2) = [ code to compute d d θ 1 J ( θ ) ] ; → 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) + λ m θ 1 gradient(3) = [ code to compute d d θ 2 J ( θ ) ] ; → 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 2 ( i ) + λ m θ 2 ⋮ gradient(n+1) = [ code to compute d d θ n J ( θ ) ] ; \begin{aligned} &\text{function [jVal, gradient] = costFunction(theta)} \\ &\text{jVal = }[ \text{code to compute } J(\theta) ]; \\ \rightarrow &J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2\\ &\text{gradient(1) = } [ \text{code to compute } \frac{d}{d\theta_0}J(\theta)]; \\ \rightarrow &\frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_0^{(i)} \\ &\text{gradient(2) = } [ \text{code to compute } \frac{d}{d\theta_1}J(\theta)]; \\ \rightarrow &\frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_1^{(i)} + \frac{\lambda}{m}\theta_1 \\ &\text{gradient(3) = } [ \text{code to compute } \frac{d}{d\theta_2}J(\theta)]; \\ \rightarrow &\frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})- y^{(i)})x_2^{(i)} + \frac{\lambda}{m}\theta_2 \\ \vdots\\ &\text{gradient(n+1) = } [ \text{code to compute } \frac{d}{d\theta_n}J(\theta)]; \\ \end{aligned} → → → → ⋮ function [jVal, gradient] = costFunction(theta) jVal = [ code to compute J ( θ )] ; J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) )) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ))] + 2 m λ j = 1 ∑ n θ j 2 gradient(1) = [ code to compute d θ 0 d J ( θ )] ; m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) gradient(2) = [ code to compute d θ 1 d J ( θ )] ; m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) + m λ θ 1 gradient(3) = [ code to compute d θ 2 d J ( θ )] ; m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x 2 ( i ) + m λ θ 2 gradient(n+1) = [ code to compute d θ n d J ( θ )] ;