Neural Network Training
神經網路已成為解決從圖像識別到自然語言處理等各種問題的重要工具。 因此,理解與神經網路相關的符號 (notation)、成本函數 (cost function) 和反向傳播算法 (backpropagation algorithm) 對於成功訓練和使用至關重要。 在本文我們還將探索反向傳播算法背後的概念,以便我們能夠更好地理解結果的含義。
Neural Networks Notation
首先我們來定義一些 notation
- = layers 數量
- = 第 l 個 layer 共有幾個 units (不含 bias unit)
- = 共有幾個 output units
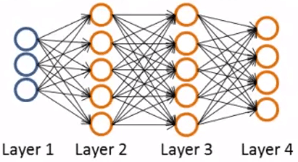
例如在上圖中
L = 4
s_1 = 3
s_2 = 5 = s_3
s_4 = s_L = 4
K = 4
- 我們又會說當 K 只有 2 時,稱作 Binary classification
- K >= 3 時,稱作 Multi-class classification
- 則拿來代表第 k 個 output
Cost Function
知道這些 notation 後我們來定義 neural networks 的 cost function
其實就只是 regularization logistic regression 的改版而已
我們還記得 Regularization logistic regression 的 cost function 是 :
而 neural networks 的 cost function 為 :
- 在前項 part1 我們加入 來加總 K 個 output nodes 的 cost
- 在後項 part2 要想辦把加總出所有的
- 所以當下的 columns 等於 sl (# of nodes in current layer)
- 而 rows 等於 sl + 1 (# of nodes in next layer)
- 於是就可以計算所有 的平方和
- 前面的 double sum 只是把每個 output nodes 的 cost 加總起來
- 後面的 triple sum 只是把 networks 中所有 平方加總起來
- triple sum 的 i 從 1 開始是為了去掉 bias unit
Backpropagation Algorithm
為了要把 Cost function 最小化,得到更好的 Update
我們首先要先取得 的微分 :
而要計算出 的微分,就是使用 Backpropagation algorithm
步驟 1
首先我們有這些 training sets
步驟 2
設定一個矩陣包含所有 l, i, j 等於 0
應該是用來存放最終的 Cost function
步驟 3
For t = 1 to m 各跑一次 Forward Propogation
- 計算
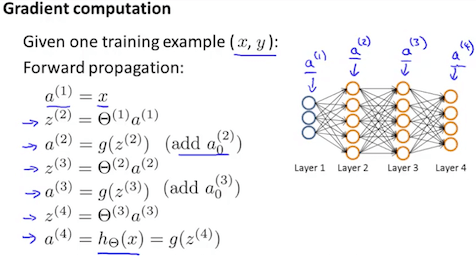
步驟 4
利用 來計算
其中的 代表最後一個 layer 的每個 activation units (output nodes)
而 代表對應 output nodes 的真正解答
所以計算出來的 就是我們 output 與解答的誤差
再來我們想從右到左倒退算出 l = L-1, L-2, ..., 2 的誤差
l = 1 不用算,因為他就是我們的 input,不會有任何誤差
步驟 5
利用 來計算前面 layers 的
計算當下 layer 的 等於
當下的 matrix 乘上 next layer 的 values
然後再 element-wise 乘上 activation function
其中這個 g-prime 又可以寫成
如此一來我們就得到了
步驟 6
將計算好的 和 帶回去
或者寫成 vectorization
最終我們得到了一個
D 可以說是 Neural networks 的 Gradient
Backpropagation Intuition
Backpropagation 看起來就像 black box 一樣,可能看不太懂
所以有一些地方需要解釋
Slope
以 binary classification (k = 1) 且不含 regularization 為例
這個 neural network 的 cost 就等於 :
而直觀的來看, 就是 的差異 (error)
還記得 derivative 在 linear 跟 logistic regression 的 cost function 中所代表的是 slope 斜率嗎 ?
而 slope 越大代表的就是我們的預測錯誤越大 !
Calculate
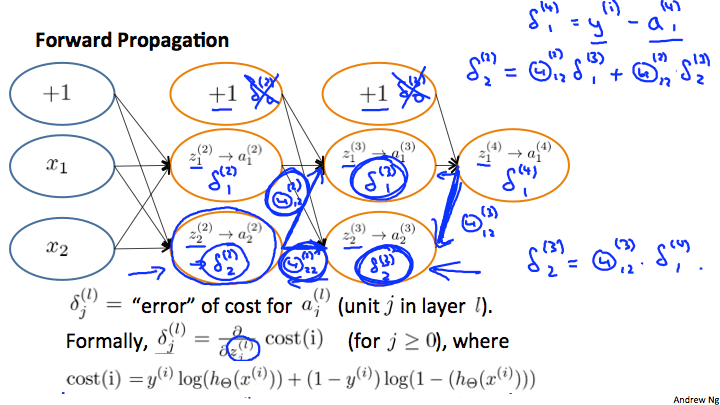
假設進行完 forward propagation 後,network 呈現上圖狀態
計算 back propogation 其實可以想成是反過來的 forward propogation
然後把 edge 想成是
或是另一個例子
Backpropogation Practices
Unrolling Parameters
在實作 neural networks 時,我們會有這些 matrices
但是很多 advanced optimization algorithm (例如 fminunc) 都需要你使用 vector 作為 inputs
所以我們必須把這些 matrices 轉成 one long vector
並在有需要時,將他們轉回 matrices
在 Octave 中,Unroll matrix to vector 方法如下 :
% Theta1 = 10x11 matrix
% Theta2 = 10x11 matrix
% Theta3 = 1x11 matrix
thetaVector = [ Theta1(:); Theta2(:); Theta3(:)]
% thetaVector = 231x1 vector
而轉回 matrices 的方法如下 :
Theta1 = reshape(thetaVector(1:110), 10, 11)
Theta2 = reshape(thetaVector(111:220), 10, 11)
Theta3 = reshape(thetaVector(221:231), 1, 11)
在 fminunc 實作中
我們會將 unroll 成 initialTheta
而在 cost function 中把他轉回 matrices
並且通過 forward propogation / backpropogation
計算出 和
而這些 D 也要 unroll 成 gradientVec 傳回
Gradient Checking
Backpropogation 有時可以發生一些意外的小 bugs
但我們可以使用 Gradient Checking 來確保 backpropogation 正確運作
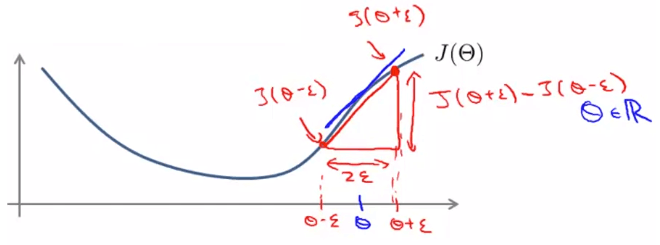
上圖假設 只是一個 real number
藍線是我們算出來的 gradient
而我們在 左右兩邊各選一個 所連起的紅線
將會是一個非常接近正確值的 gradient
這條線可以透過以下公式算出
若 是多個矩陣時
我們要針對每個 做一次 gradient checking
通常來說 即可解決問題
以下是 Octave 實作 Gradient checking :
epsilon = 1e-4;
for i = 1:n,
thetaPlus = theta;
thetaPlus(i) += epsilon;
thetaMinus = theta;
thetaMinus(i) -= epsilon;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;
計算完後,我們就可以去比較是否 gradApprox ≈ deltaVector
當你一旦確定好自己的 backpropogation 沒有 bugs 且正常運作
就應該要關掉 Gradient checking,因為他會讓程式變得非常慢 !
Random Initialization
在 Regression 設定 全為 0 是可以正常運作的
但在 Neural networks 設定所有 為 0 是無法運作的 !
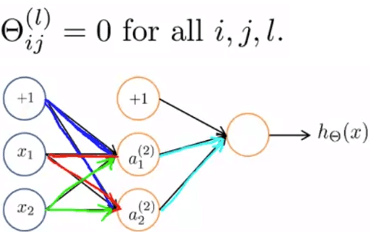
假設上圖我們藍、紅、綠的 都設為 0
那麼 就會產生一樣的結果
甚至在 和 gradient 的結果都會一樣
這讓我們的 就算怎麼更新,都會變成一樣
就像在算單個 logistic regression 但多跑了好幾個 redundant 的 features
這將會把 neural networks 的重點及優點全部都抵消掉了
Symmetric breaking
上面這個問題我們稱為 Symmetric breaking
要解決他我們將初始化所有的 隨機落於 區間
實作如下 :
% If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
以上的 不等於 gradient checking 的
Summary
首先決定一個 neural networks 的 architecture 很重要
我們必須決定以下事情 :
- number of input units
- dimension of features
- number of output units
- number of classes
- number of units in each hidden layers
- more the better, 但要考慮 computation cost
- Default : 1 hidden layer
- 如果你有大於一個 hidden layer
- 最好每層的 units 數都要一致
再來就可以來 Training a Neural Network :
- 隨機定義 Weights
- 用 forward propogation 取得
- 計算 cost function
- 用 backpropogation 取得 partial derivatives
- Gradient checking 確定 backpropogation 計算正確然後關掉 checking
- 用 gradient descent 或其他算法找到能 minimize cost function 的 weights
通常在剛接觸 neural networks 時是可以用 for loop 來 implement 的 :
for i = 1:m
forward and back propagation using example (x(i),y(i))
Get activations a(l) and delta terms d(l) for l = 2,...,L
Neural networks 的 cost function 是 non-convex 的
但通常找到的 local minimum 都還不錯 !
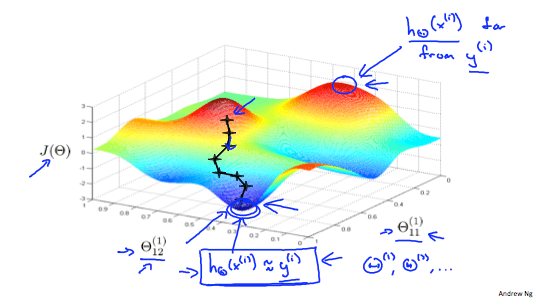
上圖就是一個 neural networks 的 visualization