Association Analysis

本文提到了關聯法則 (Association Rule) 技術，它是一種可以利用 items 之間的 occurrence 頻率，來預測一個 item 的 occurrence 機率的技術。本文針對此技術提出了定義、評估標準、例子以及優化方法，如 Brute Force approach、Apriori Algorithm，並介紹了它們之間的不同。

此外，本文亦提出了改進 Apriori Algorithm 的方法，例如 DHP（Direct Hashing & Pruning）和 Partitioning，可以減少對 database 的 scan 次數，減少 candidates 數量，並加快計算 candidate 的 support，以提高效率。此外，我們也可以使用 anti-monotone 來簡化 Rule Generation，而不必計算所有的 subset，並在 Generate Candidate rules 的時候用 shared prefix 來减少 candidates 數量。

Association Rule Mining

關聯法則 (Association Rule) 雖然在 2019 已經不是最熱門的技術，但其實他是開啟整個 Data mining 的第一把火。關聯法則就是在一堆 transaction 中，利用其他 items occurrence 的頻率，來預測我們想知道的 item 的 occurrence 機率。

Transaction Example

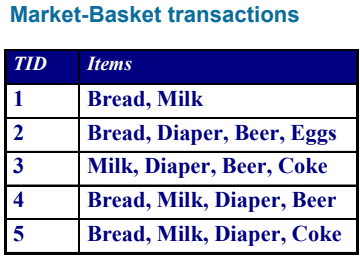
例如買尿布就會買啤酒, 買牛奶就會買雞蛋。每次預測可以包含多個 items 合在一起：

{Diaper} -> {Beer}
{Milk, Bread} -> {Eggs, Coke}
{Beer, Bread} -> {Milk}

備註

關聯法則重視的是 co-occurrence，而非 causality。也就是說，如果我們發現買了尿布就會買啤酒，這並不代表買了尿布就會造成啤酒的出現。

Definition

接下來講解一些實作中會遇到的專有名詞 :

名詞	解釋	舉例
Itemset	一或多個 item 的組合，k-Itemset 表示一個組合有 k 個 items	$\begin{Bmatrix} \text{Milk, Bread, Diaper} \end{Bmatrix}$
Support count $(\sigma)$	這一個 Itemset 在整個 transaction 中出現幾次	$\sigma(\begin{Bmatrix} \text{Milk, Bread, Diaper} \end{Bmatrix}) = 2$
Support $(s)$	該 Support count 在 transaction 的比例是多少 (ratio from 0 - 1)	$s(\begin{Bmatrix} \text{Milk, Bread, Diaper} \end{Bmatrix}) = 2/5$
Frequent Itemset	定義一個 minsup (minimum-support)，只要某個 Itemset 的 support 超過 minsup 他就是 Frequent Itemset
Association Rule	一個關聯的表達格式 $X \rightarrow Y \mid X, Y \text{ are itemsets}$	$\begin{Bmatrix} \text{Milk, Diaper} \end{Bmatrix} \rightarrow \begin{Bmatrix} \text{Beer} \end{Bmatrix}$

Rule Evaluation Metrics

要探討 Itemset 的關聯法則準確度，我們使用 Support (s) 和 Confidence (c) 來表達，Support 表示 itemset 在 transaction 出現的百分比，用 $\frac{\sigma(X, Y)}{\lvert T \rvert}$ 來表達；而 Confidence 則是指 $Y$ 有多常跟著 $X$ 一起出現，用 $\frac{\sigma(X, Y)}{X}$ 來表達。舉個例子，使用上面出現過的 transaction：

Transaction Example

如果我們想要探討 $\begin{Bmatrix} \text{Milk, Diaper} \end{Bmatrix} \rightarrow \begin{Bmatrix} \text{Beer} \end{Bmatrix}$ 的關聯度如何，我們可以用公式計算：

$$\begin{aligned} s = \frac{\sigma(\text{Milk, Diaper, Beer})}{\lvert T \rvert} = \frac{2}{5} = 0.4\\ c = \frac{\sigma(\text{Milk, Diaper, Beer})}{\sigma(\text{Milk, Diaper})} = \frac{2}{3} = 0.6 \end{aligned}$$

Full Example

接下來我們用一個更完整的例子，假設我們有一個購物網站，每個人都有一個購物車，裡面有他們想要買的東西，我們可以把他們的購物車內容記錄下來，例如：

TID	Items
100	A, C, D
200	B, C, E
300	A, B, C, E
400	B, E

• Minimum support = 2
• Minimum confidence = 2/3

則 Frequent Itemset 有 (他們都是 support 大於等於 2 的 Itemset)

{A}, {B}, {C}, {E}, {A, C}, {B, C}, {B, E}, {C, E}, {B, C, E}

而 Strong rule 為 (他們都是 confidence 大於等於 2/3 的 Itemset)

{B, E} -> {C}  (2/3)
{C} -> {A}  (2/3)
{A} -> {C}  (2/2)

Association Rule Mining Task

接著要想出一個方法在 transaction $T$, minsup, minconf 的情況下，試著找到 association rule 並滿足以下兩個條件

• $\text{support} \ge \text{minsup}$
• $\text{confidence} \ge \text{minconf}$

Brute Force approach

1. 先列出所有的 Association rules
2. 把所有 rules 的 s 和 c 都算出來
3. 再刪除所有不滿足兩條件的 rules
4. 發現不可行 (Computationally prohibitive)

Brute Force Association Rule

因為上面只考慮三個物件的 rules 就可以產生好幾種結果 (考慮賣場有上萬種商品，有幾種 Rules ?)，他們會有一樣的 support，但會有不一樣的 confidence。

Find other approach

1. 先找出所有 Frequent itemsets
2. 從這些 Frequent itemsets 再產生 strong association rules
3. 但光是找出 Frequent itemsets 又是 Computationally prohibitive

備註

通常演算法找出的 frequent itemsets 不會超過五組

Itemset Lattice

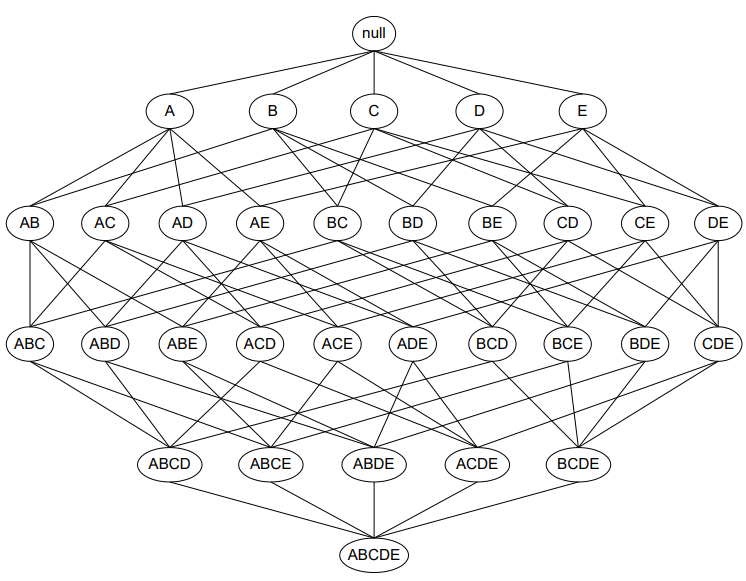
想像有 d 個 items，要將他們組成所有可能的 itemset 再從中去刪除不為 frequent 的 itemset，d 個 items 就會產生 $2^d$ 個 itemsets。

我們將 Brute force 套回來看看，因此要先產生 $M = 2^d$ 個 Candidate rules，並且在 database 掃描及更新每個 candidate rules 的 support，再將所有 transaction 比對所有 candidate rules，複雜度將會是 $O(NMw) \mid N = \text{transactions}, w = \text{itemset length}$。

Strategies

看完上面的例子，我們可以發現，我們可以從三個方向來優化

• 想辦法減少 candidate $M = 2^d$ ?
  • pruning techniques
• 想辦法減少 transactions $N$ ?
  • DHP, vertical-based mining algorithms
• 想辦法減少 comparisons $NM$ ?
  • efficient data structures

Apriori Algorithm

Principle

若 itemset 本身為 frequent itemset，那他的 subset 一定也可以是 frequent subset。意思就是任意 itemset 的 support 一定不會超過他的 subset 的 support，這個方法可以反推回我們在產生所有 itemset 的圖表中。

$$\forall X, Y : (X \subseteq Y) \Rightarrow s(X) \ge s(Y)$$

Apriori Principle Intuition

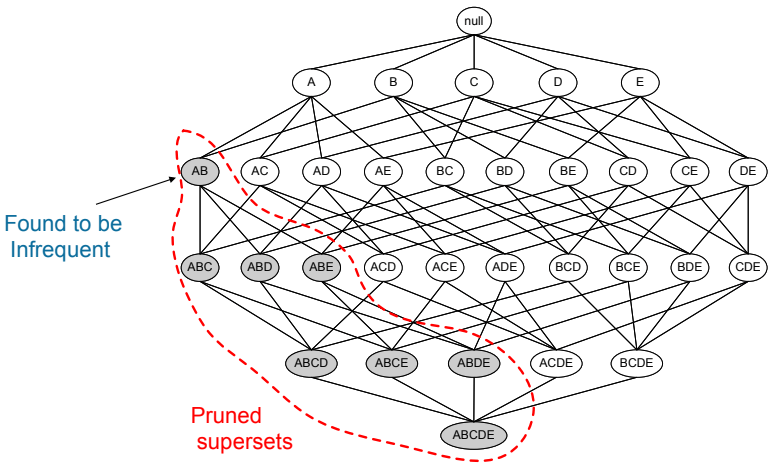
因為 itemset 的 support 一定不會超過 subset，所以若 subset 已經確定不為 frequent itemset 的話，那底下所有包含該 subset 的 itemset 都一定不會是 frequent itemset。這個原則我們稱為 Anti-monotone !

$$\begin{aligned} &\begin{Bmatrix}A, B\end{Bmatrix} \neq \text{Frequent itemset} \\ \Rightarrow &\text{Any itemset contains } \begin{Bmatrix}A, B\end{Bmatrix} \neq \text{Frequent itemset} \end{aligned}$$

Notation and Algorithm

• $C_k$ : candidate k-itemsets : 代表所有可能為 frequent 的 itemsets

• $L_k$ : frequent k-itemsets : 所有已滿足 minsup 的 frequent itemsets

• Algorithm

  k = 1, C_1 = all items
  
  While C_k not empty :
      從 C_k 找出所有符合 minsup 的放入 L_k
  
      從 L_k 產生出下一階段的 C_k+1
  
      k = k + 1

Example

Apriori Example

• 先從 $C_1$ 刪除不合 minsup 的 itemsets 產生 $L_1$
• $L_1$ 生成下一階段的 $C_2$
• $C_2$ 刪除不合 minsup 產生 $L_2$
• $L_2$ 生成下一階段的 $C_3$
• $C_3$ 刪除不合 minsup 的 itemsets 產生 $L_3$
• $L_3$ 無法再產生 $C_4$

注意在 $L_2$ 生成 $C_3$ 的時候，{Milk, Beer} 已經不是 frequent itemset，所以包含他的 {Milk, Beer, Diaper} 也不會出現在 $C_3$；如果用暴力破解，總共要產生 $\binom{6}{1} + \binom{6}{2} + \binom{6}{3} = 41$ 種 itemset，而在這個方法中，我們只產生了 $6 + 6 + 1 = 13$ 種 itemset。

Generate Candidates

在產生新的 candidate itemset 時，我們將會使用 lexicographic order 套入 SQL 中。假設現在有 $L_k$ 的 itemset，那麼新的 $C_{k+1}$ 就是由原本兩個 k-itemsets 共享了其中的 k-1 個 items。

Generate Candidate

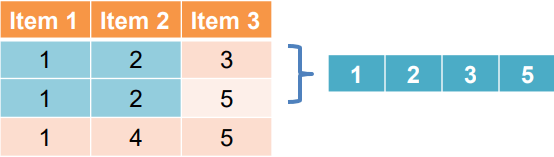
我們可以寫成 self-joining 的 SQL 語法

Generate Candidate SQL

只要前 k-1 個 items 都一樣，而最後第 k 個 item 不同，就可以產生新的 candidate。

Prune

從現在所有的 (k+1)-itemsets candidates 中去翻出每一個裡面的 subset k-itemsets 是否有 not frequent 的 itemset，如果有就要刪除該 candidate。

Challenges

看起來問題都已經解決了，但實際上仍有一些問題：

• 如何在 transaction 中進行多次掃描
• 由 $L_1$ 產生 $C_2$ 的第二層，在真實問題中會產生非常大量的 itemsets
• 計算每個 candidate 的 support (s) 非常耗費時間，但可以利用 hash tree 來加強

Subset Operation

假設我們已經有一群 candidates 的名單，我們要更新他們的 support counts。若給定 transaction 要如何產生所有 3-subset ? 我們可以使用 recursion 的方式來解決，並結合 hash tree 來加快計算。

Subset Operation

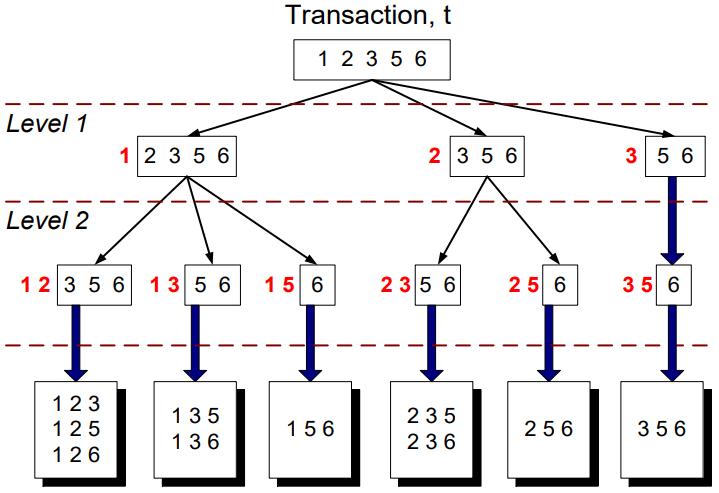
Hash tree

Hash Tree 的建法很簡單，把現有的 itemset 按照 hash function 的規則建立。其中 leaf node 用來存 itemsets & counts 的列表，而 interior node 則是存放 hash table。

Hash Function

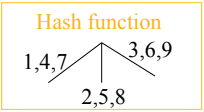
先從 item 1 開始按照 hash function 分類，當超過 max leaf size 時，就會以下一個 item 的規則分裂。

Hash Tree

最後，我們將 subset operation 套用到 hash tree 中，找到 transaction 對應的 candidates 就可以對 candidate 的 count 加一。

Subset Operation Hash Tree

備註

Other Slide

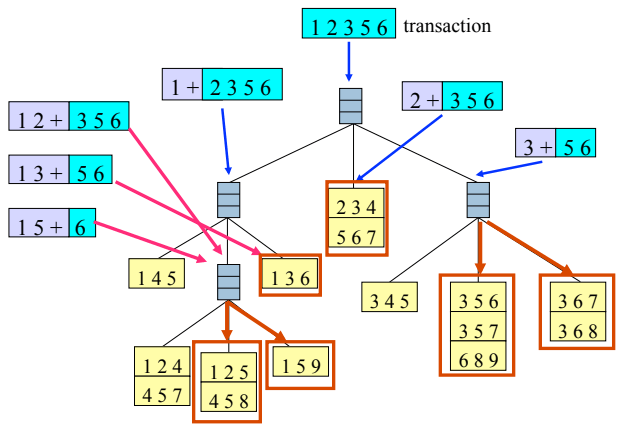
Rule Generation

我們從 frequent itemset 可以產生各式各樣的 association rules。目前為止，只要是符合 minconf 和 minsup 的 association rules，我們就會將他解釋為 good association rule。但可能有些 rules 是無用或是重複的。

Anti-monotone

在一般情形下，不同的 confidence 間是沒有 anti-monotone 的關係

$$c(ABC \rightarrow D) \;\not\!\!\!\implies c(AB \rightarrow D)$$

但是相同 itemset 所產出的 confidence 可以有 anti-monotone 的關係

$$c(ABC \rightarrow D) \ge c(AB \rightarrow CD) \ge c(A \rightarrow BCD)$$

備註

你可以想像成已知三個條件猜一個，一定比已知兩個條件猜兩個還要簡單很多。

所以當我們知道上層的 rule 是不符合 confidence 的，那相同 itemset 所產生的下層 rules 就可以被刪掉：

Lattice of Rules

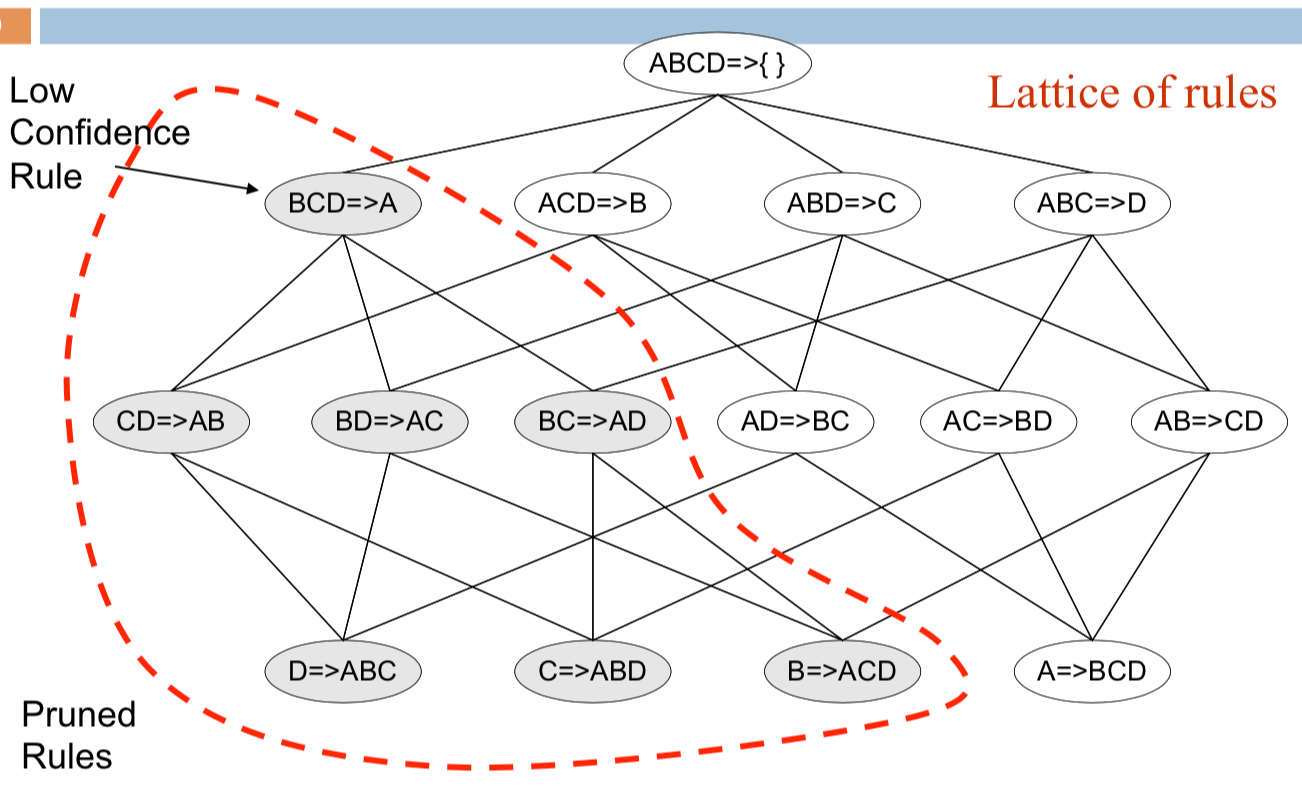
Generate Candidate rules

我們也可以用兩個 rules 來產生新的 rule，透過 shared prefix 來組成新的 rule。但若是新 rule 的 subset 含有 low confidence rule 那就必須刪除：

Rule Generation Apriori

$$\begin{aligned} &\text{join}(CD\rightarrow AB, BD\rightarrow AC) = D\rightarrow ABC \\ &\text{Prune }(D \rightarrow ABC) \text{ if } (AD \rightarrow BC) \text{ is low confidence.} \end{aligned}$$

Improvement of Apriori Algorithm

有了 Apriori Algorithm 的基礎，我們可以進一步的改進 Apriori Algorithm 來提升效率。例如：

• 減少對 database 的 scan 次數
• 減少 candidates 數量
• Facilitate support counting of candidates

DHP (Direct Hashing & Pruning)

DHP 將會運用 hashing 的技巧，將一開始的 itemsets 轉移到 hash table 上，再從 hash table 篩選出 hash 出現次數多的格子。 DHP 的目的是要改善：

• frequent itemsets generation
• transaction database size reduction
• reducing of database scans

DHP 在 hash 時可能會有誤差，但因為會不斷的往下篩選所以不要緊。

DHP Example

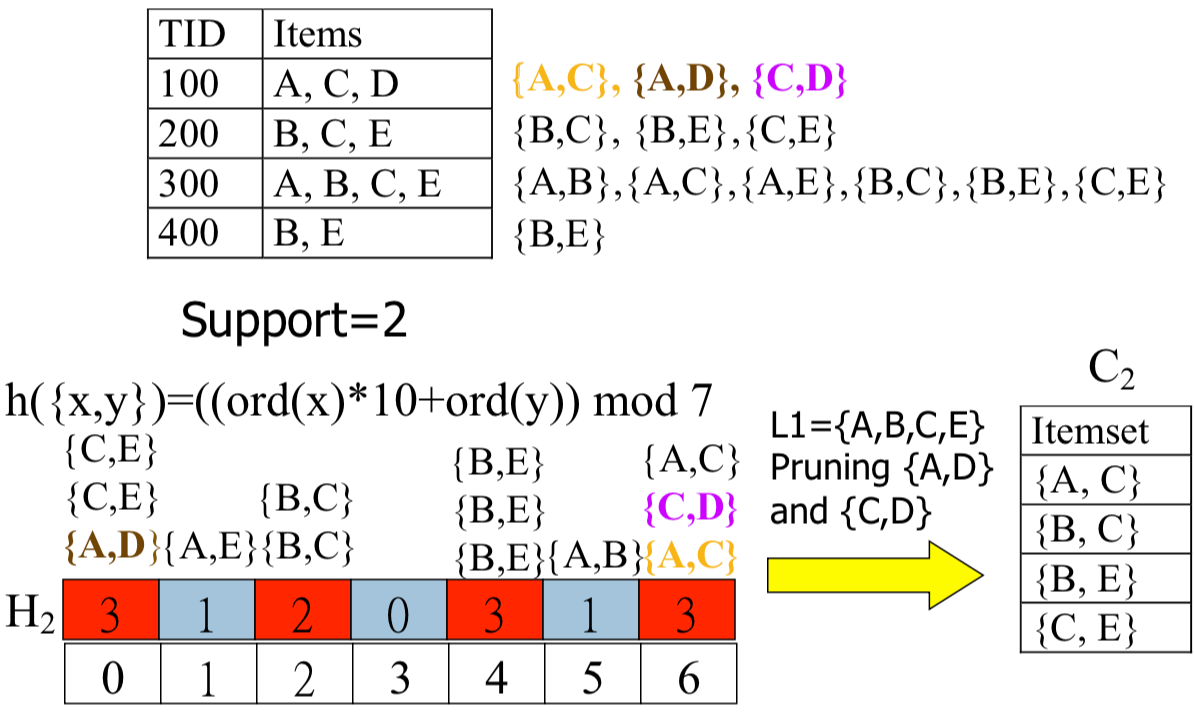
在篩選的過程中，也可以慢慢剔除掉不必要的 transactions (如 100, 400)，達到 Reduction on Transaction Database size。

Partitioning

因為 potential frequent itemset 常出現在至少一個 partition 中，所以我們將 transaction database 拆分成不重複的 partitions 放入 main memory 中：

Divide D into partitions D1, D2, ..., Dp
For i = 1 to p:
    Li = Apriori(Di)
C = L1 + L2 + ... + Lp
Count C on D to generate L

第一次 scan 時，每個 partitions 會分別產生 local frequent itemset；第二次 scan 時，collection of local frequent itemset 就能找出 global candidate itemset。每一個 partitions 能夠平行化運算增加效率，但還是會在第二次 scan 時產生過多的 candidates。

Beyond Apriori Algorithm

所以 Apriori 始終沒辦法解決 candidates 過多的問題，我們有辦法避免 candidate generation 嗎？