跳至主要内容

Other Association Rules

本文探討了其他 Association Rules，包括 Multilevel Association Rules、Closed Association Rules、Quantitative Association Rules，以及從 Association Mining 到 Correlation Analysis 的關聯性。

文中提到了如何使用 uniform support、reduced support 來更準確的找到 association rules；以及可以使用 one-hot encoding 來做編碼，以及一些對 quantitative data 適用的 mining methods。此外，還有可以對 item 添加 weight 比重以及使用 inter-transaction association rules 來提升效率，或是使用 constraints 來改善 Association Rules 的效率。

Multilevel Association Rules​

Items 之間有 hierarchy，lower level 為 lower support，且 transaction 可以透過 level 來加上 encoding。

Multilevel Association Rules
Multilevel Association Rules

Uniform Support​

不會因為 ancestor 沒通過 minsup 就不檢查他的子樹，但如果 uniform support 設定太高，可能會遺失掉 low level association，如果設定太低則可能產生太多 high level association。

備註

The same minimum support for all levels

Reduced Support​

以四種策略動態決定 low level 的 minimum support，跟現實生活較接近 (例如商品單價改變可能影響 support)

  • Level-by-level independent
  • Level-cross filtering by single item
  • Level-cross filtering by k-itemset
  • Controlled level-cross filtering by single item

Closed Association Rules​

  • max pattern : 一個 frequent itemset 沒有比他更大的 frequent itemset
  • Closed Frequent itemset : itemset X 要符合兩件事才是 closed itemset
    • 找不到任何 proper superset Y
    • 找不到任何 superset Y 出現在所有 X 也出現的 transaction
Closed Frequent Itemsets
Closed Frequent Itemsets

例如 {e} 在每個 transaction 都找不到其他的 item 同時出現，因此可以獨立成為一個 closed frequent itemset，例如當 a 在 100 與 200 都有，但是卻沒有一起出現在 300 時。

Maximal Frequent Itemset​

若 itemset 沒有任何的 superset 是 frequent，那它就是 maximal frequent itemset。

Maximal Frequent Itemset
Maximal Frequent Itemset

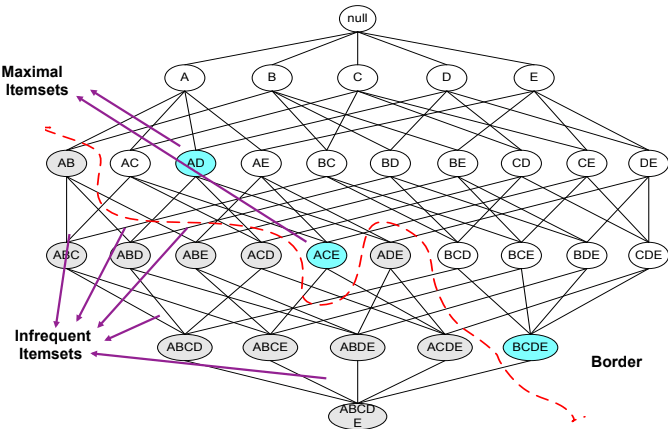
Maximal vs. Closed Itemsets​

我們可以用 lattice 綜觀所有的 itemset 發現：

  • 當 superset 的 item 都沒有重複跟自己一起出現的，那就是 closed itemset
  • 當 superset 的 support 皆小於自己，那就是 maximal itemset

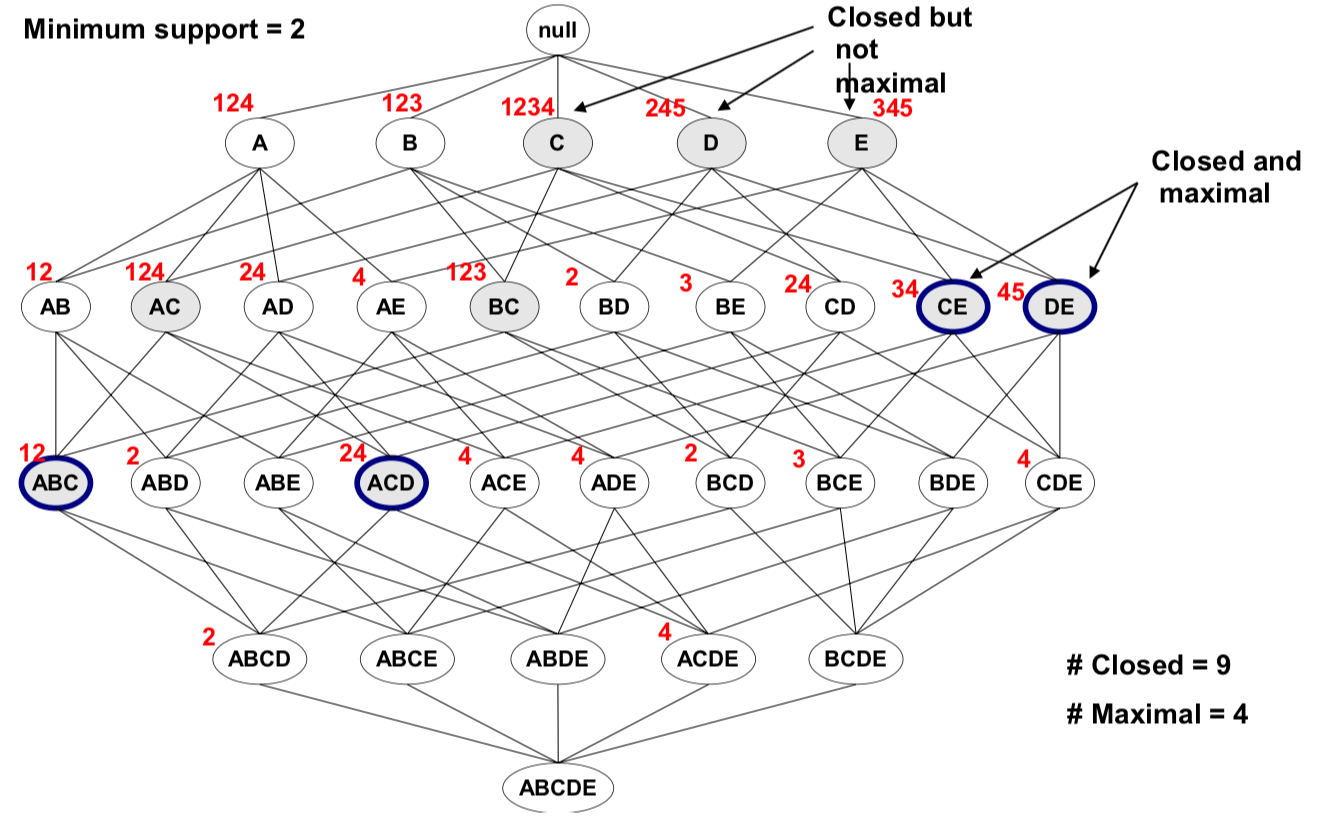
我們可以用 maximal & closed 來過濾當 minsup 設定太低時，所出現的 itemset，它們雖然通過 minsup 但沒有用處，總結一下 :

Maximal Frequent Itemsets⊂Closed Frequent Itemsets⊂Frequent Itemsets\text{Maximal Frequent Itemsets} \subset \text{Closed Frequent Itemsets} \subset \text{Frequent Itemsets}

Quantitative Association Rules​

當 attributes 從 boolean 變為 continuous space 時，應該如何使用 Association rules ?

Multidimensional Association Rules​

例如 attributes 變為 categorical (有限個選項) 或 numerical (不斷變化的數值)

age(30−35)∧income(30K−50K)→buys(HDTV)\text{age}(30-35) \wedge \text{income}(30K-50K) \rightarrow \text{buys}(HDTV)

Example​

Record IdAgeMarried# cars
10023No1
20025Yes1
30029No0
40034Yes2
50038Yes2

我們可以將 age 進行離散化可以得到

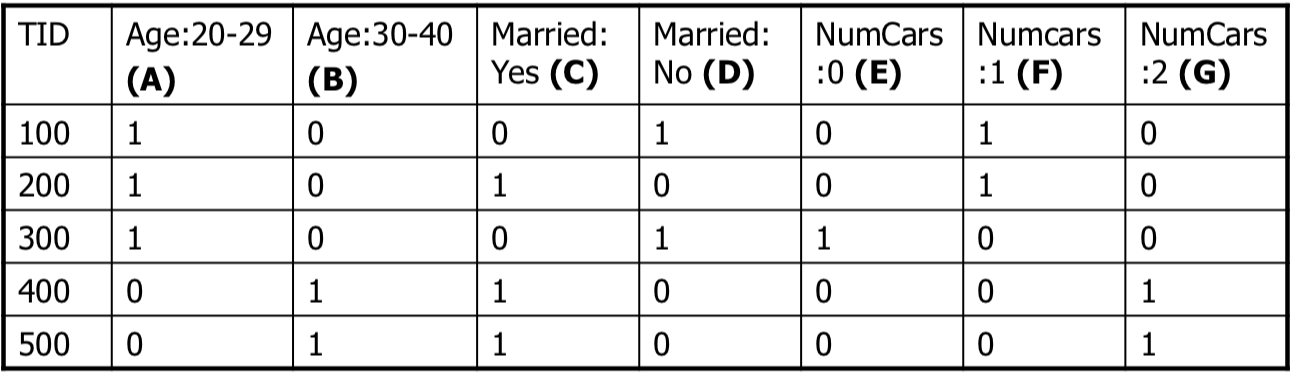
Map Boolean Rules
Map Boolean Rules

然後整理成為一般的 transactions

TIDItems
100A,D,F
200A,C,F
300A,D,E
400B,C,G
500B,C,G

但離散化的 minsup 和 minconf 可能較難設定

One Hot Encoding​

另外在處理此類 Quantitative association 時，編碼的方式也非常重要。例如要處理此類 attributes：

{male, female}
{europe, us, asia}
{firefox, chrome, safari, ie}

假設我們要取得 {male, us, safari}。 傳統編碼把每個 itemset 都從 0 編碼，可以得到 {0, 1, 2}，這種編碼方法可能造成 distance 之類的錯誤。 而 one hot encoding 會將每個 itemset 只取一個作為 true 值，得到 {10, 010, 0010}。

Mining methods​

以下有幾種方法適合用來對 quantitative data 進行 mining：

  • Static discretization of quantitative attributes
    • Discretized prior to mining using concept hierarchy.
    • Numeric values are replaced by ranges.
    • Data cube (n dimensional cuboid 對應 n predicate sets)
  • Quantitative association rule
    • Discretized based on distribution of data
    • Numeric attributes are dynamically discretized
    • 2D grid to predict
  • Distance-based association rule
    • Discretized based on semantic meaning of interval
    • Different binning methods
    • Consider density/number and closeness in an interval

From Association Mining to Correlation Analysis​

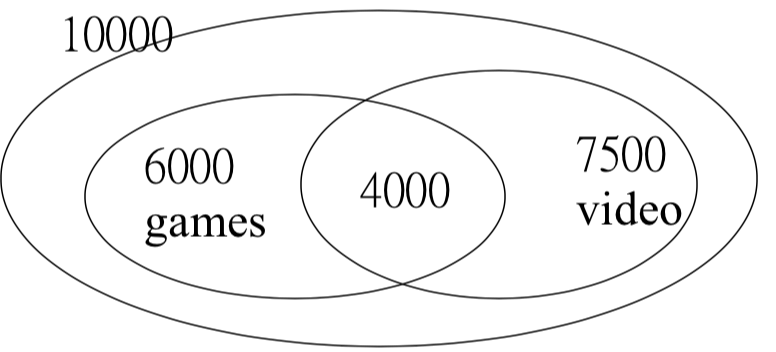
Uncorrelation Rules
Uncorrelation Rules

考慮上圖關聯 Games  ⟹  Videos\text{Games} \implies \text{Videos}，雖然 confidence 很高：

support =4000/10000=0.4confidence =4000/6000=0.66\begin{aligned} \text{support } = 4000/10000 = 0.4\\ \text{confidence } = 4000/6000 = 0.66 \end{aligned}

因為 videos 本身的出現率就已經有 0.75 之高，所以用購買 Games 來推測出還會購買 Videos 的方法，反而還降低機率，算是 negatively associated。

Correlation Analysis​

我們可以使用 Correlation 的方式來推測 rules 是不是夠 strong

Corr(A,B)=P(A∪B)/(P(A)×P(B))\text{Corr}(A, B) = P(A \cup B) / (P(A) \times P(B))
  • 若 Corr(A, B) = 1 代表兩者完全無關 (independent)
  • 若 Corr(A, B) > 1 代表 A 對 B 有 positive 的 correlation
  • 若 Corr(A, B) < 1 代表 A 對 B 只有 negative 的 correlation

用 Games, Videos 來算算看可以得到 :

Corr(Games, Videos)=0.4/0.6∗0.75=0.89\text{Corr(Games, Videos)} = 0.4 / 0.6 * 0.75 = 0.89

Weighted item​

另外我們還可以對 item 添加 weight 比重，讓比重較高的 item 需要多一點重視，所以會較容易出現在 rules 中。例如我有五種 itemsets 以及七筆 transactions：

Weighted Itemset
Weighted Itemset

那麼 {B, E} 的新 support 可以這樣算 : (0.3+0.9)∗5/7=0.86(0.3+0.9)*5/7 = 0.86

Inter-transaction association rules​

  • Intra-transaction association rules
    • 當某些 item 出現變化時
    • 特定的 item 也會 同時 出現變化 constraints
    • IBM 跟 SUN 漲價，此時 Microsoft 就會一起漲價
  • Inter-transaction association rules
    • 當某些 item 出現變化時
    • 特定的 item 就是下一個出現變化的 item
    • IBM 跟 SUN 漲價，而 Microsoft 隔天就會漲價

Association Rules with Constraints​

  • 一般的 association rules 可能缺乏 user exploration 跟 focus
  • 或是一遇到海量資料就會失效
  • 這時候就要依靠定義 constraints，例如 :
    • Data constraints: SQL-like queries
    • Dimension/level constraints
    • Rule constraints
    • Interestingness constraints
  • 有兩種 rule constraints
    • rule from constraints
      • P(x,y)∧Q(x,w)  ⟹  Buy(x,"Education software")P(x, y) \wedge Q(x, w) \implies \text{Buy}(x, \text{"Education software"})
    • rule (content) constraints
      • Sum(S.price<5)\text{Sum}(S.\text{price} < 5)