跳至主要内容

Sequence Pattern

本文主要介紹了 Sequence Pattern Mining，它是一種用於找出在時間軸上 Item 之間的 Association Rule 的方法，而我們將一般 Dataset 加上 Timeline 來取得 Sequence Data Table，並且使用 Apriori-based SP algorithm (GSP) 等算法來找出所有的 Frequent Subsequence，再來提出了 Episode Mining 以及 FreeSpan 和 PrefixSpan 演算法，以更有效率的方式找出 Frequent Subsequence。

Sequence Data​

在前一章節的 Association Analysis 中，itemset 都是固定一筆一筆所出現。若我們想要更了解 Item 之間的 association rule，勢必要加上時間軸，得到順序與因果關係。我們可以將一般 Dataset 加上 Timeline 取得 sequence data table

Sequence Data Table
Sequence Data Table
ObjectTimestampEvents
A102,3,5
A206,1
A231
B114,5,6
B172
B217,8,1,2
B281,6
C141,8,7

Definition​

名詞說明
Sequence我們的時間軸，時間軸上有許多 elements
Element即 transaction，一個 transaction 有許多 events
Event每個 events 代表一個 item
Length of sequence用 ∣s∣\lvert s\rvert 表達 sequence 上的 elements 有幾個。k-sequence 代表該 sequence 上共有 k 個 events

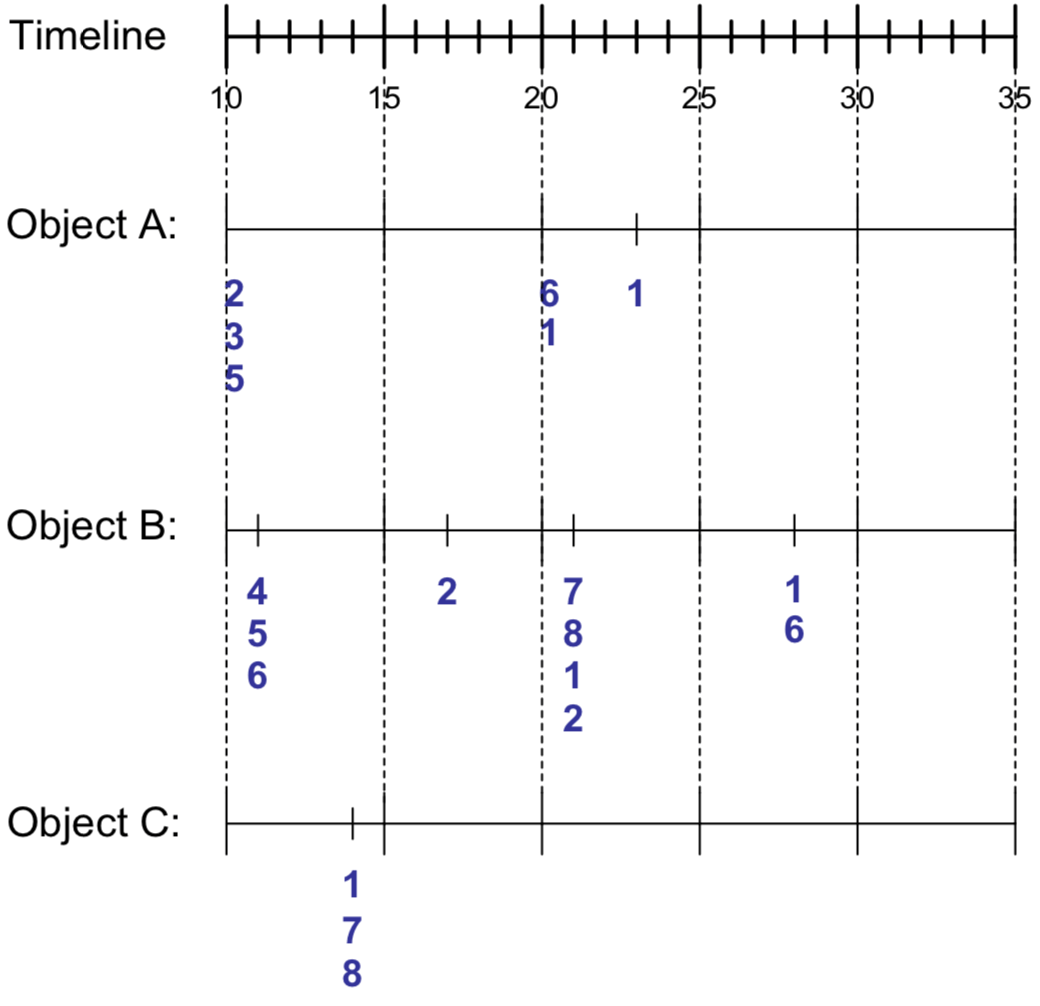
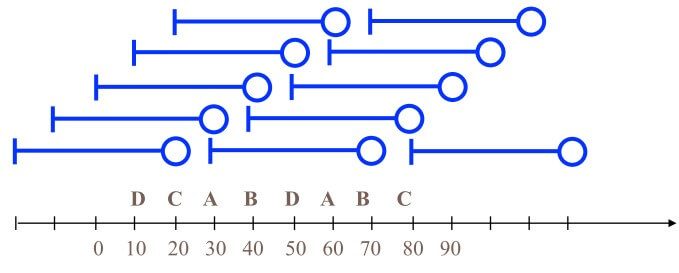
舉例來說，下圖是一個 8-sequence with length 5 的 sequence data：

Sequence Data
Sequence Data

還有許多的例子

  • web sequence <{Homepage} {Electronics} {Cameras} {Shopping Cart} ... >
  • library checkout books <{Fellowship of the Ring} {The Two Towers} {Return of the King}>

Subsequence​

如果序列 A 的每個元素的事件都是另一個序列 B 對應的元素的子集，那麼序列 A 就是 B 的子序列 (subsequence)。

Subsequence Example
Subsequence Example

一個 subsequence 的 support 等於 data sequences 包含該 subsequence 的比例。求 Sequential pattern 等於是求 Frequent subsequence，也就是 support ≥\ge minsup 的 subsequence。

Sequential Pattern Mining​

Sequential Pattern Mining 就是從一群 sequences 中找出所有的 frequent subsequences。

我們這邊使用 <a(bc)dc> 來表示有四個 elements 分別為 a, bc, d, c。而他是 <a(abc)(ac)d(cf)> 的 subsequence：

<a( bc)    d c>
<a(abc)(ac)d(cf)>

現在我們要從這個 sequence database 找出 sequential pattern

Find Sequential Pattern
Find Sequential Pattern

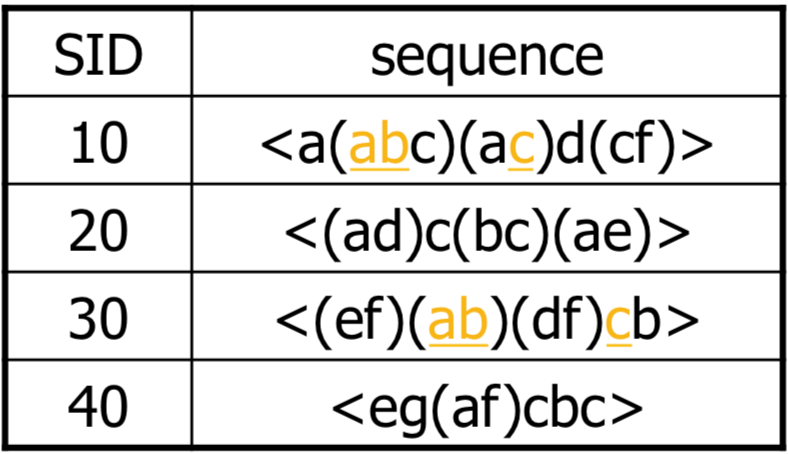
假設 minsup = 2，那我們可以找到 <(ab)c> 是一個 sequential pattern，因為 (ab) 跟 c 都有出現過兩次。

Definition of Sequential Pattern Mining​

Given :
    1. a database of sequences
    2. a minsup

Task :
    1. find all subsequences with support >= minsup

Extracting sequential patterns method​

首先，直覺上可以用 candidates + apriori 的方法來找出 subsequences。這類的方法有： Apriori* (Apriori All, Apriori Some)、Apriori-based SP algorithm (GSP)。但有一些問題：

  1. 會產生過多的 candidate sequences
  2. database scans 次數過多
  3. 要找的 sequential patterns 長度越大越困難
Extract Subsequences
Extract Subsequences

Sequential Pattern Mining Algorithm​

  1. 首先將 data 進行 sorting
  2. 計算 large itemset 也就是 support 值
  3. 進行 transformation (Replacement)
  4. sequence phase
  5. maximal phase

Example​

進行 sorting 後產生以下資料

Sequential Pattern 1
Sequential Pattern 1

找出滿足 support 的 large itemset，並給他們定義一個新 id

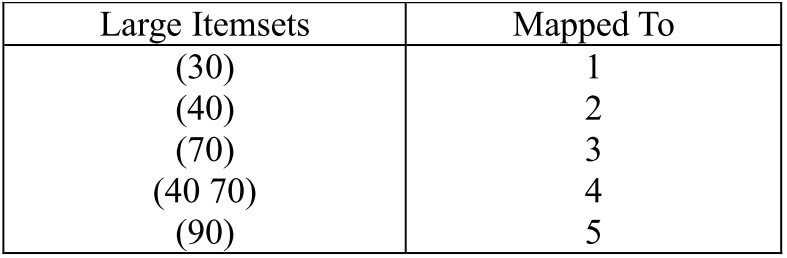
Sequential Pattern 2
Sequential Pattern 2

在 Transformation Phase，我們刪除原本資料不滿足 support 的 item。將滿足的資料能攤開的攤開，然後設定新 id

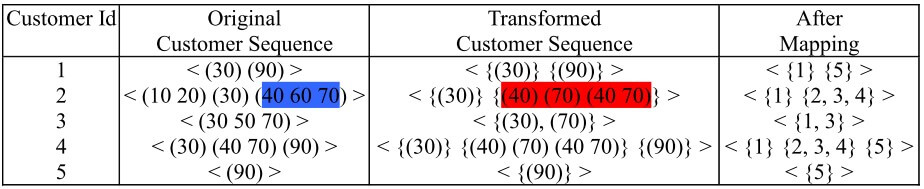
Sequential Pattern 3
Sequential Pattern 3

在 Sequence Phase，將 after mapping 的 items 攤開成 Maximal Large Sequence (Apriori-like)

<1 2 3> : support = 2
<1 2 4> : support = 2

Generate <1 2 3 4>

最後 Maximal Sequence，找出 sequence 沒有包含在其他 sequence 即為 maximal sequence。

e.g.

<(3) (4 5) (8)> is contained by <(7) (3 8) (9) (4 5 6) (8)>

<(3) (5)> is not contained by <(3 5)>

Episode Mining​

  • Episode : A partially ordered collection of events occurring together
  • 以 sliding window 方式來抓出 sequence
  • discover all frequent episodes from a given class(ex. all parallel or all serial) of episodes
Episode Mining
Episode Mining

FreeSpan​

  • Frequent pattern-projected Sequential pattern mining
    • 將 sequence database 投影成較小的 projected database
    • grow subsequence fragments in each projected database
    • Divide-and-conquer

Example​

FreeSpan 1
FreeSpan 1
  • a 皆出現在這四筆所以 a : 4
  • 以此類推求出所有 support > 2 的 item 並排序
f_list = a:4, b:4, c:4, d:3, e:3, f:3
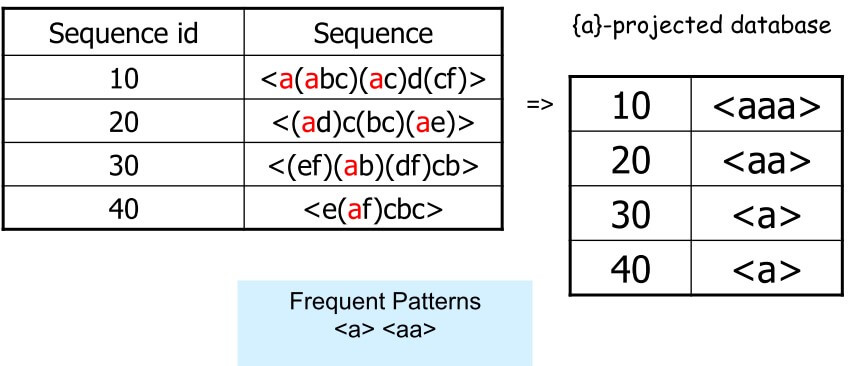
FreeSpan 2
FreeSpan 2
  • 先對 a 投影
    • aaa 只出現 1 次所以不拿
    • aa 出現 2 次
    • a 出現 4 次
FreeSpan 3
FreeSpan 3
  • 以 a 為底，接著對 b 投影
    • 可以抓出 b 出現 4 次
    • ab 出現 4 次
    • (ab) 出現 2 次
    • 要注意 ab 和 (ab) 是不同的
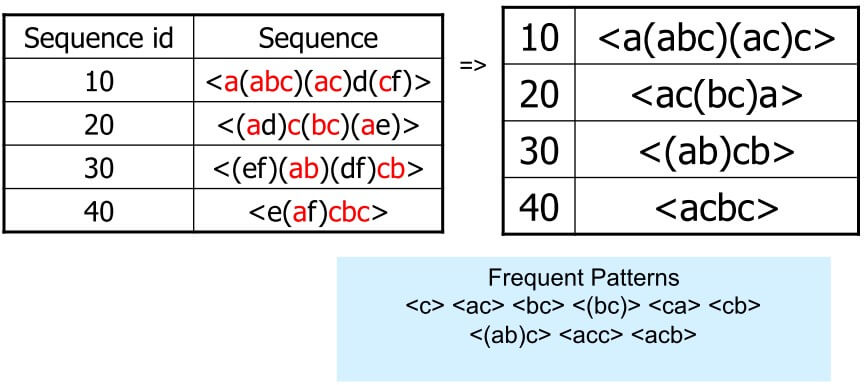
FreeSpan 4
FreeSpan 4
  • 以 a, b 為底，接著對 c 投影

PrefixSpan​

  • Prefix-projected Sequential pattern mining
    • 一樣是 Projection-based
    • less projections and quickly shrinking sequences
  • PrefixSpan 有三個核心，分別是 prefix, postfix, projection
    • 假設有一 sequence 為 <a(abc)(ac)d(cf)>
    • Prefix
      • <a>, <aa>, <a(ab)>, <a(abc)> ...
      • 一定要從每一個 item 的頭開始
      • 所以 <ab>, <a(bc)> 這些都不算在 prefix
    • Postfix
      • 對於 <aa> 來說他的 postfix 為
        • <(_bc)(ac)d(cf)>
      • 對於 <bd> 來說他的 postfix 為
        • <(cf)>
    • Projection
      • projection 讓我們可以 groupby
      • <bd> 的 projection 是 <bd(cf)>

Example​

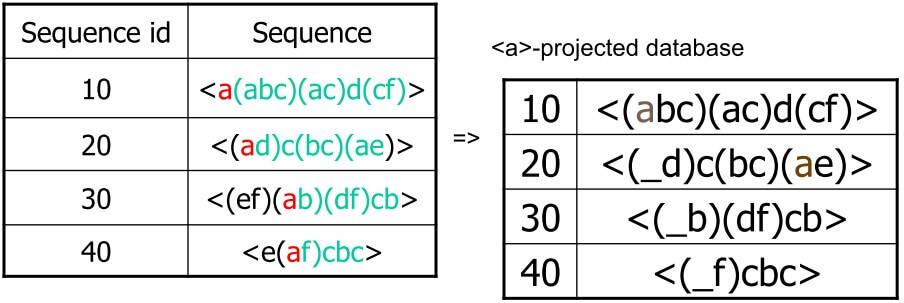
PrefixSpan 1
PrefixSpan 1
  • 先對 a 投影，就可以找出所有有 prefix a 的 length 2 sequence
    • <aa>:2 <ab>:4 <(ab)>:2 <ac>:4 <ad>:2 <af>:2
    • 接著就可以對這 6 個 subsets 遞迴投影
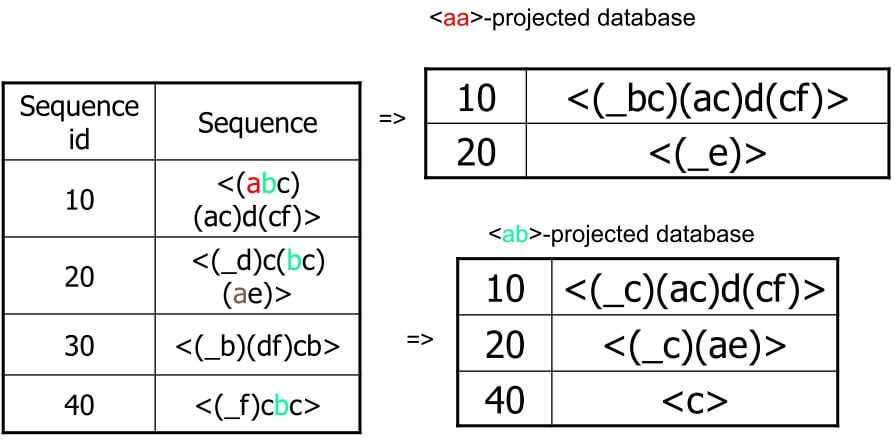
PrefixSpan 2
PrefixSpan 2
  • 例如對 <aa> 投影，有兩筆可以繼續遞迴
  • 對 <ab> 投影，有三筆可以繼續遞迴
  • 同時也可以刪去不滿足 support 的 item
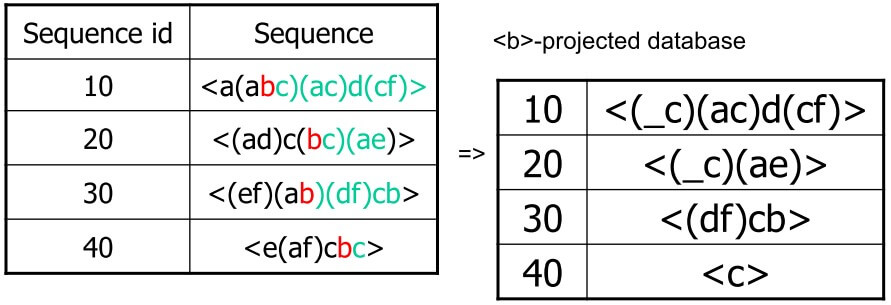
PrefixSpan 3
PrefixSpan 3
  • 將 a 及其 subsets 進行一輪後
  • 接著就可以對 b 及他的 subsets 投影