FP-growth

FP-growth 的主要目的是破解 candidate generation 所引起的 bottleneck，因此將不會用到任何 candidate generation，並且在 main memory 實作以減少對 database 的 scans，主要的概念是 divide-and-conquer，並且利用了 suffix tree 的概念。

Suffix Tree

Keyword Trees

將 keywords 儲存在 rooted labeled tree。每個從 root 到 leaf 的 path 都會對應一個 keyword。利用 "threading" 技巧 traverse 文章找出 keywords，每當我們走到了 leaf node 就代表找到 keyword。

Keyword Tree

Suffix Tree

運用 keyword tree 的概念利用文字的字尾 (suffixes) 來建立一種 trie data structure，其 leaves 會是每個 suffix 在文章的 start position。

Build a Suffix Tree

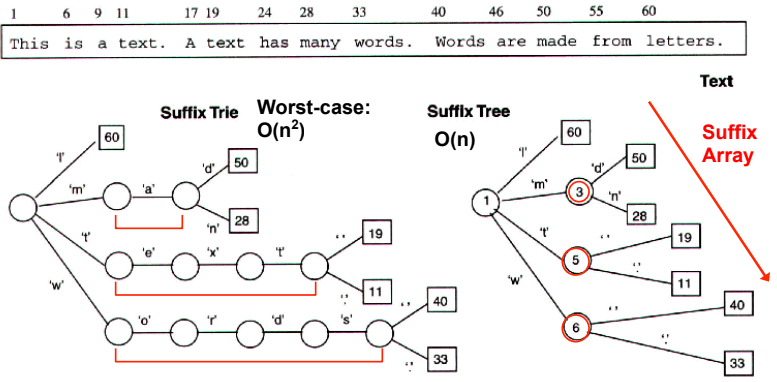
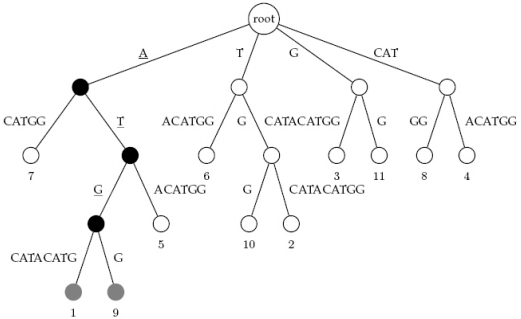
Suffix tree 可以掌握所有文字的 suffixes，並且只需要 $O(\text{length})$ 的時間就能建立 tree。例如，下面是一個將基因序列索引成 suffix tree 的例子：

Example of Suffix Tree

FP-Growth Algorithm

以下是 FP-growth 的演算法，主要分成兩個步驟：

1. Construct FP-Tree (Frequent pattern tree)
2. FP-Growth (Frequent pattern growth)
   1. 根據不同 frequent item 將 FP-tree 分裂成 Conditional FP-Tree
   2. 針對每一個 conditional FP-Tree 進行 mining

FP-Trees Construction

先 scan 所有 1-itemset 的 support ，但要 sort 成 descending order。排序可以改變 transaction 結構，幫助我們用更少 nodes 來建樹。

FP-Tree Construction Step 1

FP-Tree Construction Step 2

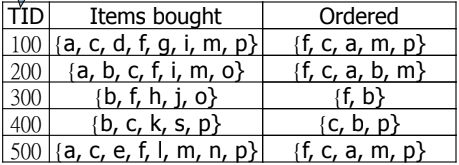
將 ordered 的 itemset 建立成 FP-tree。從第一筆開始建樹，一樣的 character 就加一，不一樣的 character 就建立分支。

FP-Tree Construction Step 3

最後，將 tree 中相同 character 從 header table 串連起來。

FP-Tree Construction Step 4

FP-Growth

接續上面產生的 FP-Tree，我們先從每一個 1-itemset 來建立 Conditional Pattern Base (由下往上)，例如 p 可以從 fcam (2 次) 接過來，也可從 cb (1 次) 接過來。

接著從 conditional pattern base 建立出 Conditional FP-Tree，找出在 conditional pattern base 有相同 prefix 的 items，並且可以符合 minsup。例如 p 的 fcam 跟 cb 代表 $c \rightarrow p$ 共有出現 3 次。

最後，我們將 conditional FP-Tree 找到的 items 各自拆開與原本的 item 結合，例如 $c \implies (c \rightarrow p)$。

FP-Growth

備註

A complete FP-Growth Example

FP-Growth Advantages

FP-Growth Advantages include the use of the divide-and-conquer technique to decompose mining and the database, as well as no need for candidate generation, a compressed database (FP-Tree), no repeated scans of the database, and no pattern searching and matching.