Multivariate Linear Regression Multivariate linear regression 是指當 linear progression 有多個 features (variables) 時,就可以稱作為 multivariate linear regression。舉例來說,可以使用 size, ages, number of bedrooms, floors 來判斷 house price,此時我們可以將 Hypothesis 寫成:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \cdots + \theta_nx_n h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n 接著,我們可以使用 Gradient Descent 來解決 Multivariate linear regression 的 cost function,為了更好的運作,可以使用 feature scaling 或是 mean normalization 的方法來達到減少 iteration 的效果。
當 linear progression 可以有多個 features (variables) 時
稱作 Multivariate linear regression
例如一次用 size, ages, number of bedrooms, floors 來判斷 house price
size bedrooms floors age price 2104 5 1 45 460 1416 3 2 40 232 1534 3 2 30 315
此時我們多了一些名詞 :
n = number of features x ( i ) = the features (input) of the i t h training example x j ( i ) = value of feature j in the i t h training example \begin{aligned} n &= \text{number of features}\\ x^{(i)} &= \text{the features (input) of the } i^{th} \text{ training example}\\ x^{(i)}_j &= \text{value of feature j in the } i^{th} \text{ training example} \end{aligned} n x ( i ) x j ( i ) = number of features = the features (input) of the i t h training example = value of feature j in the i t h training example 用表格來舉例 :
m = 3 n = 4 x ( 2 ) = [ 1416 3 2 40 ] x 3 ( 3 ) = 2 \begin{aligned} m &= 3 \\ n &= 4 \\ x^{(2)} &= \begin{bmatrix} 1416 \\ 3 \\ 2 \\ 40 \end{bmatrix} \\ x^{(3)}_3 &= 2 \end{aligned} m n x ( 2 ) x 3 ( 3 ) = 3 = 4 = ⎣ ⎡ 1416 3 2 40 ⎦ ⎤ = 2 我們的 Hypothesis 也不再是單純的
h θ ( x ) = θ 0 + θ 1 x h_\theta(x) = \theta_0 + \theta_1x h θ ( x ) = θ 0 + θ 1 x 而可以是 :
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \cdots + \theta_nx_n h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n 我們可以用房子當作例子來想像這個公式 :
h θ ( x ) = 80 + 0.1 x 1 + 0.01 x 2 + 3 x 3 − 2 x 4 h_\theta(x) = 80 + 0.1x_1 + 0.01x_2 + 3x_3 - 2x_4 h θ ( x ) = 80 + 0.1 x 1 + 0.01 x 2 + 3 x 3 − 2 x 4 代表 80 為房價的基底 0.1 為 size 的權重 0.01 為 bedroom 數量的權重 以此類推,最終將會得出一個 solid value for pricing 我們可以使用矩陣和向量來簡化 Hypothesis
首先我們先假設 x0 來補齊每一個 training set 對應的 base value (80 的部分)
x 0 ( i ) = 1 x^{(i)}_0 = 1 x 0 ( i ) = 1 所以 features 可以建成一個 n + 1 size 的 vector
x = [ x 0 x 1 x 2 ⋮ x n ] ∈ R n + 1 \begin{aligned} x = \begin{bmatrix} x_0 \\ x_1 \\x_2 \\\vdots\\x_n \end{bmatrix} \in \mathbb{R}^{n+1} \end{aligned} x = ⎣ ⎡ x 0 x 1 x 2 ⋮ x n ⎦ ⎤ ∈ R n + 1 而 parameters 也一樣可以建成一個 n + 1 size 的 vector
θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] ∈ R n + 1 \begin{aligned} \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\\theta_2 \\\vdots\\\theta_n \end{bmatrix} \in \mathbb{R}^{n+1} \end{aligned} θ = ⎣ ⎡ θ 0 θ 1 θ 2 ⋮ θ n ⎦ ⎤ ∈ R n + 1 如此一來, Hypothesis 可以寫成
x 0 = 1 , h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n = [ θ 0 θ 1 ⋯ θ n ] [ x 0 x 1 ⋮ x n ] = θ T x \begin{aligned} x_0 &= 1,\\ h_\theta(x) &= \theta_0x_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \cdots + \theta_nx_n\\ &= \begin{bmatrix} \theta_0 & \theta_1 & \cdots & \theta_n \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n \end{bmatrix} \\ &= \theta^Tx \end{aligned} x 0 h θ ( x ) = 1 , = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n = [ θ 0 θ 1 ⋯ θ n ] ⎣ ⎡ x 0 x 1 ⋮ x n ⎦ ⎤ = θ T x Multivariate 不只會讓 Hypothesis 改變,也會讓 Cost function 改變 :
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 J ( θ ) = 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) 2 甚至可以寫成 :
J ( θ ) = 1 2 m ∑ i = 1 m ( ( ∑ j = 0 n θ j x j ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}((\sum_{j=0}^n\theta_jx^{(i)}_j) - y^{(i)})^2 J ( θ ) = 2 m 1 i = 1 ∑ m (( j = 0 ∑ n θ j x j ( i ) ) − y ( i ) ) 2 或是寫成 :
J ( θ ) = 1 2 m ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(\theta^Tx^{(i)} - y^{(i)})^2 J ( θ ) = 2 m 1 i = 1 ∑ m ( θ T x ( i ) − y ( i ) ) 2 在看新的 Gradient descent algorithm 前,先複習原本只有一個 feature 的算法 :
Repeat until convergence: θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) ( simultaneously update θ 0 , θ 1 ) \begin{aligned} \text{Repeat} &\text{ until convergence: }\\ &\theta_0 := \theta_0 - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})\\ &\theta_1 := \theta_1 - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x^{(i)}\\ &(\text{simultaneously update }\theta_0, \theta1) \end{aligned} Repeat until convergence: θ 0 := θ 0 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) θ 1 := θ 1 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) ( simultaneously update θ 0 , θ 1 ) 而新的 Gradient descent algorithm 其實非常簡單 :
Repeat until convergence: θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) θ 2 : = θ 2 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 2 ( i ) ⋯ ( simultaneously update θ 0 , θ 1 , ⋯ θ n ) \begin{aligned} \text{Repeat} &\text{ until convergence: }\\ &\theta_0 := \theta_0 - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_0^{(i)}\\ &\theta_1 := \theta_1 - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_1^{(i)}\\ &\theta_2 := \theta_2 - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_2^{(i)}\\ &\cdots\\ &(\text{simultaneously update }\theta_0, \theta1, \cdots \theta_n) \end{aligned} Repeat until convergence: θ 0 := θ 0 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) θ 1 := θ 1 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) θ 2 := θ 2 − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 2 ( i ) ⋯ ( simultaneously update θ 0 , θ 1 , ⋯ θ n ) 因為我們已經定義過, x0 = 1,所以才可以這樣寫
代表每一個微分項裡面都會有乘上對應的 feature
我們可以將算法再簡化一些 :
Repeat until convergence: θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) for j = 0 ⋯ n (and update simultaneously) \begin{aligned}\text{Repeat} &\text{ until convergence: }\\ &\theta_j := \theta_j - \alpha \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}\\ & \text{for j = } 0 \cdots n \text{ (and update simultaneously)} \end{aligned} Repeat until convergence: θ j := θ j − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) for j = 0 ⋯ n (and update simultaneously) 這就是解決 Multivariate linear regression 的 cost function 的 Gradient descent algorithm
現在來學習幾個方法來改善 gradient descent 的一些小缺點
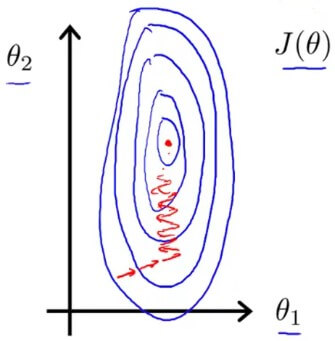
我們發現若 feature 的數值範圍若過大,會造成 cost function 所形成的 contour plot 變成類似橢圓形
Feature scaling reason 而 gradient descent 將會以較慢速度,來回擺動直到找到最佳收斂點
所以 feature 值盡量介於以下區間 (當然不是必須,但不要差太多就行) :
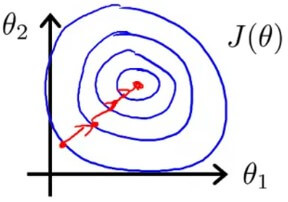
− 1 ≤ x i ≤ 1 or − 0.5 ≤ x i ≤ 0.5 \begin{aligned} -1 \le x_i \le 1 \\ \text{or}\\ -0.5 \le x_i \le 0.5 \end{aligned} − 1 ≤ x i ≤ 1 or − 0.5 ≤ x i ≤ 0.5 有兩個方法可以解決問題,分別是 feature scaling 和 mean normalization
讓 gradient descent 可以良好的運作在類圓形的 cost function,減少 iteration 的次數
Feature scaling fix Feature scaling 將 input feature 除以 range (例如 features 的 maximum - minimum 或是 standard deviation)
來讓新的 input value 變成接近在 1 範圍的新數值
例如 :
x 1 = size ( feet 2 ) 2000 x 2 = number of bedrooms 5 \begin{aligned} x_1 &= \frac{\text{size} (\text{feet}^2)}{2000} \\ x_2 &= \frac{\text{number of bedrooms}}{5} \end{aligned} x 1 x 2 = 2000 size ( feet 2 ) = 5 number of bedrooms Mean normalization 則是將 input 減去 features average
來讓新的 input value 接近 zero mean (x0 = 1 不會變)
我們會將兩個方法合而為一個公式 :
x i : = x i − μ i S i x_i := \frac{x_i - \mu_i}{S_i} x i := S i x i − μ i 其中 mu 代表是所有 features 的平均值 S 表示 Range 值 (or standard deviation) 例如 :
Housing prices 在 range 2000 ~ 5000 然後 mean value 為 1000
所以每個新的 features 會計算為 :
x i : = x i − 1000 3000 x_i := \frac{x_i - 1000}{3000} x i := 3000 x i − 1000 要確保 gradient descent 正常運作
我們可以使用以下的 plot 進行 debugging gradient descent :
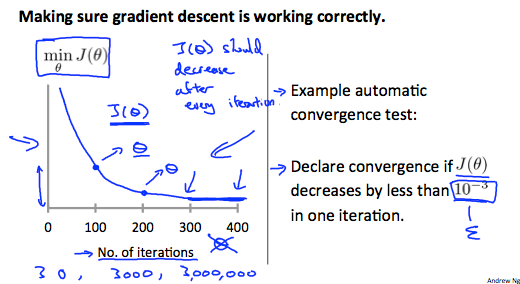
Gradient descent debug x 軸為 gradient descent 已經 iterate 的次數 y 軸為 cost function 的表現 如果 J function 是往上增加
可能是 gradient descent algorithm 寫錯了 或需要把 alpha 值減少再重做一遍 不同問題的 gradient descent 所需要的 iteration 數也不同
可能從幾百到幾百萬次迴圈數都有可能
所以這張圖可以很清楚的看到 gradient descent 的狀態
另外也可以使用 Automatic convergence test
透過設置一個小於 10^-3 的值,並觀察下一次的 iteration 是否變動小於該數
來自動告訴我們已經收斂
但要設置這個數是較困難的,所以比較少使用
至少已經證明
當 learning rate alpha 夠小
cost function J 是會不斷 decrease 的
Gradient descent observe 所以當 debug plot 發生這幾種現象時
應考慮減少 alpha 值
我們可以改變 features 以及 Hypothesis 的形式及組成
來優化 Hypothesis 讓他適應更多不同的 training sets
像是我們可以組合兩個 features 為一個,透過簡單的相乘即可 :
x = x 1 ⋅ x 2 x = x_1 \cdot x_2 x = x 1 ⋅ x 2 例如使用房子的 width 和 height 作為 features 時
h θ ( x ) = θ 0 + θ 1 ⋅ frontage + θ 2 ⋅ depth h_\theta(x) = \theta_0 + \theta_1 \cdot \text{frontage} + \theta_2 \cdot \text{depth} h θ ( x ) = θ 0 + θ 1 ⋅ frontage + θ 2 ⋅ depth 我們可以將兩者相乘得到 area 作為新的 feature :
x (area) = frontage ⋅ depth h θ ( x ) = θ 0 + θ 1 ⋅ x \begin{aligned} x \text{ (area)} &= \text{frontage } \cdot \text{ depth} \\ h_\theta(x) &= \theta_0 + \theta_1 \cdot x \end{aligned} x (area) h θ ( x ) = frontage ⋅ depth = θ 0 + θ 1 ⋅ x Hypothesis 也不一定只能使用 linear function 來 fit training sets
我們可以將 hypothesis function 轉為 quadratic, cubic 或 square root function 甚至是更多不同的 functions
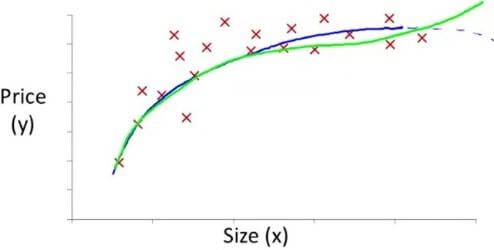
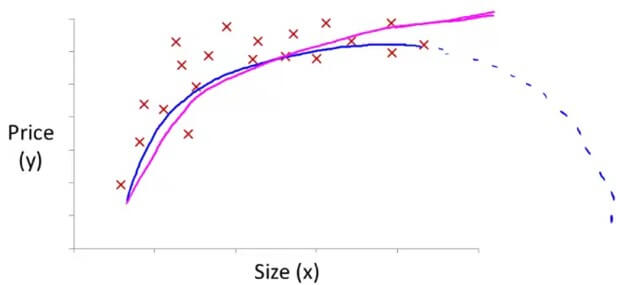
Polynomial regression - quadratic 例如上面這一個 training sets 若使用一般的 linear function 一定不好
我們可以使用藍線的 quadratic function
只要將同一個 feature 拿來平方即可
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 2 h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_1^2 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 2 但 quadratic 會在 size 越大時得到更少 price
所以我們可以使用綠線的 cubic function
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 2 + θ 3 x 1 3 h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_1^2 + \theta_3x_1^3 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 2 + θ 3 x 1 3 這時候有兩個新的 feature 就是由 x1 的平方和立方求得
要十分注意的是 !
這類 Polynomial regression 在搭配 feature scaling 時
數值的範圍改變非常重要 !
例如 :
Range of x 1 = 1 − 1000 \text{Range of }x_1 = 1 - 1000 Range of x 1 = 1 − 1000 那麼在 quadratic 及 cubic 的部分就會變成 :
Range of x 1 2 = 1 − 1 , 000 , 000 Range of x 1 3 = 1 − 1 , 000 , 000 , 000 \begin{aligned} \text{Range of }x_1^2 &= 1 - 1,000,000 \\ \text{Range of }x_1^3 &= 1 - 1,000,000,000 \end{aligned} Range of x 1 2 Range of x 1 3 = 1 − 1 , 000 , 000 = 1 − 1 , 000 , 000 , 000 其實上面用 quadratic 跟 cubic function 都沒有非常 fit
最後,我們用一個 square root 的例子來練習
Polynomial regression - square root 也就是上圖紫線的部分
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2\sqrt{x_1} h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 而他在 feature scaling 後的 features 就是 (不考慮 mean normalization) :
x 1 = size 1000 , x 2 = size 1000 x_1 = \frac{\text{size}}{1000}, x_2 = \frac{\sqrt{\text{size}}}{\sqrt{1000}} x 1 = 1000 size , x 2 = 1000 size