Normal Equation

有一種方法可以不用透過迭代尋找最小化成本函數 (cost function) 的參數 (parameters)，這種方法稱為 Normal equation，只要將訓練集 (training sets) 的特徵 $x$ 與結果 $y$ 轉換為矩陣，就能套用 normal equation 直接得到最佳解。

$$\theta = (X^TX)^{-1}X^Ty \mid \theta \in \mathbb{R}^{n+1}$$

以房價預測為例：特徵將會加上 $x_0$ 組成矩陣 $X$ ，而已知的結果將會組成向量 $y$。

Normal Equation Example

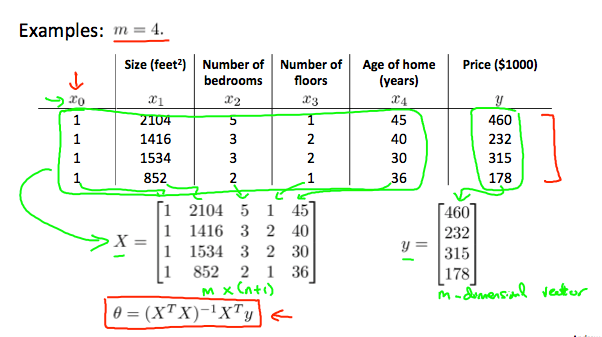
在 Octave 中要實作 normal equation 的語法如下，其中的 pinv 為求反矩陣，而 X' 則為求矩陣轉置 (transpose)。

pinv(X'*X)*X'*y

Difference between Gradient Descent and Normal Equation

Gradient Descent	Normal Equation
Alpha	No alpha
Iteration	No iteration
O(kn^2)	O(n^3)
n 可以很大	n 很大會變慢

備註

Normal equation 不需要 Feature scaling

但 normal equation 的 n (features) 不能很大。當 n 超過 10,000 時，最好使用 gradient descent 取代。

Normal Equation Noninvertibility

事實上，Octave 中要計算反矩陣有兩種方法：inv 和 pinv，其中 pinv 不管有沒有 invertible 都會返回一個反矩陣，但若 $X^TX$ 不是 invertible 的話，可能會出現使用了多餘特徵（Redundant features）或是特徵數量太多超過 training sets 的數量 (m < n) 的問題，所以可以從這兩點先來修改，應該可以優化計算。