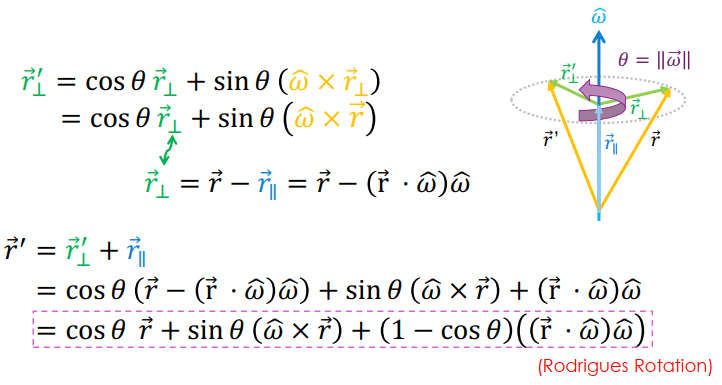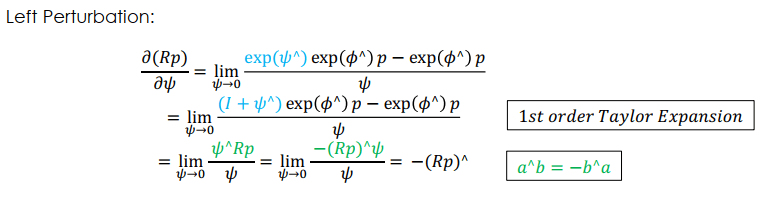跳至主要内容

Lie group and Lie algebra

本文介紹了 Lie Group 和 Lie Algebra，他們可以用來解決 3D 時的最佳化問題，特別是計算 Rotation Matrix。Lie Group 是把所有合法的 Rotation Matrix 集合起來稱為 Special Orthogonal Group (SO)，以及如果想描述 Translation 時就要加入 t 來組成 Special Euclidean group (SE)。而 Lie Algebra 由 Φ\Phi 組成，與 Lie Group 的切線空間對應。

Motivation​

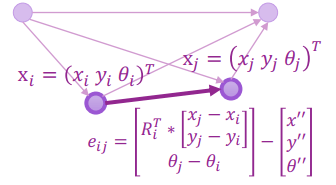
還記得我們要求 Graph Optimization for 2D Pose 的時候，需要計算 rotation 嗎 ? 這個 Rotation 在 2D 時可以用 θ\theta 簡單表示就好，但在 3D 時會變得非常複雜，且無法簡單求導數 (原因是 rotation matrix 是無法使用加法運算的)。

Graph Optimization for 2D Error
Graph Optimization for 2D Error

在 3D 時我們只可以在 manifold space 解決 rotation matrix 的最佳化。而 rotation 有很多種表達方式:

  • Rotation matrix
  • Euler Angles
  • Axis-angle
  • Quaternion
  • Etc.
Manifold Space
Manifold Space

Axis-Angle​

用 Axis-angle 舉例，定義旋轉軸 ω\omega 跟旋轉角度 θ=∥ω⃗∥\theta = \lVert \vec{\omega}\rVert。其中 r′r' 是 rr 延著旋轉軸 ω\omega 進行 θ\theta 度旋轉後的向量，可拆成平行和垂直於 ω\omega 的向量 (水平不會改變，可以沿用舊的)。最後可以得到 rodrigues rotation 公式: 在 axis-angle 下用舊的向量來取得新的旋轉向量。

Axis-angle
Axis-angle

Group​

把所有合法的 rotation matrix 集合起來稱為 Special Orthogonal Group (SO)，其中 R 要是 orthogonal 且 det = 1。例如當 R 在三維空間時為 SO(3)：

SO(3)={R∈R3×3∣RRT=I,det⁡(R)=1}SO(3) = \left\{ \mathbf{R}\in \mathbb{R}^{3\times3} \mid \mathbf{RR^T = I}, \det(\mathbf{R}) = 1 \right\}

當你不只描述 rotation 還想描述 translation 時就要加入 t，因為連續的轉換太麻煩，用更簡潔的方式 T 來表達整個 transformation：

[a′1]=[Rt0T1][a1]=defT[a1]\begin{aligned} \begin{bmatrix} \mathbf{a}' \\1 \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ 0^T & 1\end{bmatrix} \begin{bmatrix} \mathbf{a}\\ 1\end{bmatrix} \overset{\mathrm{def}}{=} \mathbf{T}\begin{bmatrix} \mathbf{a} \\ 1\end{bmatrix} \end{aligned}

合法的 T 一樣可以組成 group，稱為 Special Euclidean group (SE)，必須滿足 R 在 SO 且 t 為合法向量，例如當 T 在三維空間時為 SE(3)：

SE(3)={T=[Rt0T1]∈R4×4∣R∈SO(3),t∈R3}\begin{aligned} SE(3) = \left\{ T = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ 0^T & 1\end{bmatrix} \in \mathbb{R}^{4\times 4} \mid \mathbf{R} \in SO(3), t\in \mathbb{R}^3 \right\} \end{aligned}

Definition of Group​

Group 的基本定義，必須滿足以下四點：

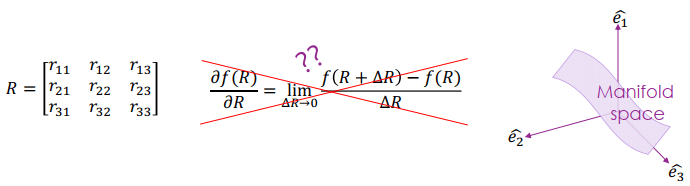
  • closure: 進行 binary operation 還在同空間
  • identity
  • inverse
  • associativity (結合律)

因為用簡單的三維矩陣來表達 rotation matrix，加法不滿足 group 的定義，無法進行導數，所以必須尋找替代方案

Interpolating Rotation Matrices
Interpolating Rotation Matrices

Lie Group​

Lie Group 裡的每個元素都是連續的，要解決 manifold space 的最佳化，就要了解 lie group 和 mapping 對應的 lie algebra。現在有一個任意的 rotation matrix 滿足 orthogonal (RRT=I\mathbf{RR^T = I})，且跟著時間 t 改變 (R(t)\mathbf{R(t)})。我們發現對 R(t)R(t)T=I\mathbf{R(t)R(t)^T = I} 中的 t 做導數，會得到一個反對稱矩陣。

  • ∧\wedge 代表建構反對稱 (antisymmetric) 矩陣
  • ∨\vee 代表從反對稱矩陣中，推回三維向量矩陣
a∧=A=[0−a3a2a30−a1−a2a10],A∨=a=[a1a2a3]\begin{aligned} \mathbf{a}^{\wedge} = \mathbf{A} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0\end{bmatrix}, \quad \mathbf{A}^{\vee} = \mathbf{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3\end{bmatrix} \end{aligned}

對 t 做導數，得到的反對稱矩陣記為 Φ(t)\Phi(t)，R˙(t)R(t)T=Φ(t)∧\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}=\Phi(t)^{\wedge}，可以從 ϕ(t)\phi(t) 推回得到 R(t)\mathbf{R(t)} 的一階導數結果：

R˙(t)=ϕ(t)∧R(t)=[0−ϕ3ϕ2ϕ30−ϕ1−ϕ2ϕ10]R(t)\begin{aligned} \dot{\mathbf{R}}(t)=\boldsymbol{\phi}(t)^{\wedge} \mathbf{R}(t)=\left[\begin{array}{ccc} 0 & -\phi_{3} & \phi_{2} \\ \phi_{3} & 0 & -\phi_{1} \\ -\phi_{2} & \phi_{1} & 0 \end{array}\right] \mathbf{R}(t) \end{aligned}

而 ϕ(t0)\phi(t_0) 其實就是 SO(3) 在原點附近的正切空間

Lie Algebra​

ϕ(t0)=ϕ0R˙(t)=ϕ(t)∧R(t)=ϕ0∧R(t)\boldsymbol{\phi}\left(t_{0}\right)=\boldsymbol{\phi}_{0} \quad \dot{\mathbf{R}}(t)=\boldsymbol{\phi}(t)^{\wedge} \mathbf{R}(t)=\boldsymbol{\phi}_{0}^{\wedge} \mathbf{R}(t)

因為知道怎麼求 R(t)\mathbf{R(t)} 微分，就可以求得 R(t)=exp⁡(ϕ0∧t)\mathbf{R(t)} = \exp (\boldsymbol{\phi}^\wedge_0 t)。很多個 Φ\Phi 可以組成 Lie algebra，這些 Φ\Phi 必須可以形成反對稱矩陣：

Φ=ϕ∧=[0−ϕ3ϕ2ϕ30−ϕ1−ϕ2ϕ10]∈R3×3sd(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}\begin{aligned} &\Phi=\phi^{\wedge}=\left[\begin{array}{ccc} 0 & -\phi_{3} & \phi_{2} \\ \phi_{3} & 0 & -\phi_{1} \\ -\phi_{2} & \phi_{1} & 0 \end{array}\right] \in \mathbb{R}^{3 \times 3}\\ &\mathfrak{s} \mathfrak{d}(3)=\left\{\boldsymbol{\phi} \in \mathbb{R}^{3}, \boldsymbol{\Phi}=\boldsymbol{\phi}^{\wedge} \in \mathbb{R}^{3 \times 3}\right\} \end{aligned}

Lie algebra 代表的就是 Lie group 的切線空間，也要滿足一些特性，其中的 binary operation 為 Lie bracket (外積可以是其中一種)

  • closure
  • bilinearity
  • alternativity
  • jacobi identity

對 Lie algebra 中由 Φ\Phi 而來的反對稱矩陣 A 取 exp 就可以對應回 lie group 的某個 R

exp⁡(A)=∑n=0∞=1n!An\exp(A) = \sum_{n=0}^\infty = \frac{1}{n!}A^n

這個對 A 取 exp 就像在 Axis-Angle 的 Rodrigues Rotation 一樣在做 rotation 的描述

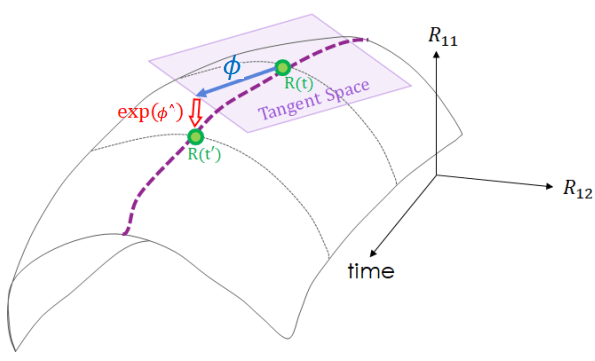
Lie Group vs. Lie Algebra​

Lie Group vs. Lie Algebra
Lie Group vs. Lie Algebra
  • Rotation matrix 是特殊的 lie group
  • Rotation matrix 會有一個對應的 lie algebra (R 的切線空間)
  • 可以用 exponential, logarithmic 來做 mapping
Lie Group vs. Lie Algebra
Lie Group vs. Lie Algebra
  • 上圖顯示 lie group, lie algebra 的對應關係
  • Lie group = manifold space
  • 沿著時間 rotation 會不斷改變
  • 在時間 t 可以找到切平面 ϕ\phi (lie algebra 裡的一個元素)
  • 用 ϕ\phi 求反對稱矩陣，就能求得新的 rotation matrix

Perturbation Model​

因為對 lie algebra 求導太複雜，有比較簡單的做法稱為 perturbation model

Perturbation Model
Perturbation Model

最後可以得到更新 R 的方法

Rnew=exp⁡(ψ∧)RinitR_{\text{new}} = \exp(\psi^{\wedge}) R_{\text{init}}