跳至主要内容

SLAM Back-end I

本文介紹了 SLAM 的後端技術，主要涵蓋 Kalman Filter、Extended Kalman Filter 和 EKF-SLAM，它們都是用來預測未知環境並更新位置的算法。Kalman Filter 是一種基於線性和高斯分布的演算法，而 Extended Kalman Filter 則是在原本的 Kalman filter 上加入線性近似的概念，最後結合 EKF 用於 SLAM 的技術就是 EKF-SLAM，它將 pose 和 landmark 整合起來定義成狀態，並重新定義 prediction 以及 observation model。

Kalman Filter​

機器人透過 prior 分布 (原本就預測的目的地, xkprex_k^{\text{pre}}) 和 likelihood 分布 (感應地標後得到的目的地, xkobsx_k^{\text{obs}})

Robot Prior Likelihood
Robot Prior Likelihood

結合兩個分布就能得到 posterior 分布 (最終決定移動的點, xkestx_k^{\text{est}})

Robot Posterior
Robot Posterior

以下是 kalman filter 對狀態的建模

Kalman Filter
Kalman Filter
  • x-axis: 時間方向
  • y-axis: 可觀察、不可觀察
  • Noise 的分布 (Q, R) 在假設中皆為高斯分布 (Gaussian distribution)
  • Goal: 用可觀察的東西，對不可觀察的東西做出預測

假設所有變換都是線性的，可以得到以下公式:

xk=Axk−1+Buk+wkzk=Hxk+vk\begin{aligned} &x_{k}=A x_{k-1}+B u_{k}+w_{k}\\ &z_{k}=H x_{k}+v_{k} \end{aligned}

Kalman Filter Computation Steps​

共有四個參數: A,B,Q,RA, B, Q, R

  1. 預測下一個狀態
xkpre=Axk−1est+Bukx_{k}^{p r e}=A x_{k-1}^{e s t}+B u_{k}
  1. 計算預測的 covariance
Pkpre=APk−1estAT+QP_{k}^{p r e}=A P_{k-1}^{e s t} A^{T}+Q
  1. 計算 Kalman-gain
Kk=PkpreHT(HPkpreHT+R)−1K_{k}=P_{k}^{p r e} H^{T}\left(H P_{k}^{p r e} H^{T}+R\right)^{-1}
  1. 預測狀態的 mean
xkest=xkpre+Kk(zk−Hxkpre)x_{k}^{e s t}=x_{k}^{p r e}+K_{k}\left(z_{k}-H x_{k}^{p r e}\right)
  1. 預測狀態的 covariance
Pkest=(I−KkH)PkpreP_{k}^{e s t}=\left(I-K_{k} H\right) P_{k}^{p r e}

Extended Kalman Filter​

Kalman filter 線性以及高斯分布的假設讓所有運算都變得簡單

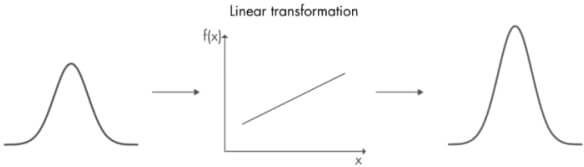Kalman Filter Distribution
Kalman Filter Distribution

但在現實中的狀況大多不是這麼簡單

Kalman Filter Distribution in Reality
Kalman Filter Distribution in Reality

於是在 Kalman filter 上加入"線性近似"的概念，就得到了 extended Kalman filter，也就是在預測狀態的 mean 時，改用 1st order Taylor expansion 來求

Extended Kalman Filter Taylor
Extended Kalman Filter Taylor

可以看到藍色線就是求得的近似線性值，我們可以得到新的公式:

  • Prediction Model \& Observation Model
xk=f(xk−1,uk)+wkzk=h(xk)+vk\begin{aligned} &x_{k}=f\left(x_{k-1}, u_{k}\right)+w_{k}\\ &z_{k}=h\left(x_{k}\right)+v_{k} \end{aligned}
  • Jacobian Matrix:
Fk=∂f(x^k−1,uk)∂x,Hk=∂h(x^k)∂xF_{k}=\frac{\partial f\left(\hat{x}_{k-1}, u_{k}\right)}{\partial x}, H_{k}=\frac{\partial h\left(\hat{x}_{k}\right)}{\partial x}
  • Linearized System
xk=f(x^k−1,uk)+Fk(xk−1−x^k−1)+wkzk=h(x^k)+Hk(xk−x^k)+vk\begin{aligned} &x_{k}=f\left(\hat{x}_{k-1}, u_{k}\right)+F_{k}\left(x_{k-1}-\hat{x}_{k-1}\right)+w_{k}\\ &z_{k}=h\left(\hat{x}_{k}\right)+H_{k}\left(x_{k}-\hat{x}_{k}\right)+v_{k} \end{aligned}

Extended Kalman Filter Computation Steps​

在原本的 Kalman filter 時，計算中的 A, H 都是固定的，而在 EKF 中，每個時間點都須根據前一刻的估計值，重新用第一階的 taylor expansion 求得線性近似:

xkpre=f(xk−1est,uk)Pkpre=FkPk−1preFkT+QKk=PkpreHT(HPkpreHT+R)−1xkest=xkpre+Kk(zk−Hxkpre)Pkest=(I−KkH)Pkpre\begin{aligned} &x_{k}^{p r e}=f\left(x_{k-1}^{e s t}, u_{k}\right)\\ &P_{k}^{\text {pre}}=F_{k} P_{k-1}^{\text {pre}} F_{k}^{T}+Q\\ &K_{k}=P_{k}^{p r e} H^{T}\left(H P_{k}^{p r e} H^{T}+R\right)^{-1}\\ &x_{k}^{e s t}=x_{k}^{p r e}+K_{k}\left(z_{k}-H x_{k}^{p r e}\right)\\ &P_{k}^{e s t}=\left(I-K_{k} H\right) P_{k}^{p r e} \end{aligned}

EKF-SLAM​

為了將 EKF 應用到 SLAM 問題中，首先要將 pose, landmark 定義成狀態 (state)

sk=(x,y,θ⏟robot’s pose,m1,x,m1,y⏟landmark 1,m2,x,m2,y⏟landmark 2,…,mn,x,mn,y⏟landmark n)Ts_{k}=\left(\underbrace{x, y, \theta}_{\text{robot's pose}}, \underbrace{m_{1, x}, m_{1, y}}_{\text{landmark 1}}, \underbrace{m_{2, x}, m_{2, y}}_{\text{landmark 2}}, \ldots, \underbrace{m_{n, x}, m_{n, y}}_{\text{landmark n}}\right)^{T}

而狀態的分布如下，其中 covariance 可以拆成四個部分 (pose 本身關聯、pose 和 map 關聯、map 本身關聯)

[xyθm1,xm1,y⋮mn,xmn,y]→μ=[xm],Σ=[ΣxxΣxmΣmxΣmm]\begin{aligned} \left[\begin{array}{c} x \\ y \\ \theta \\ m_{1,x} \\ m_{1,y} \\ \vdots \\ m_{n,x} \\ m_{n,y} \end{array}\right] \rightarrow \mu=\left[\begin{array}{c} \mathbf{x} \\ \mathbf{m} \end{array}\right], \Sigma=\left[\begin{array}{cc} \Sigma_{\mathbf{x x}} & \Sigma_{\mathbf{x m}} \\ \Sigma_{\mathbf{m x}} & \Sigma_{\mathbf{m m}} \end{array}\right] \end{aligned}

Prediction Model​

  • Prediction Model
[x′y′θ′]=[xyθ]+[−vωsin⁡(θ)+vωsin⁡(θ+ωtΔt)vωcos⁡(θ)−vωcos⁡(θ+ωtΔt)ωΔt]\begin{aligned} \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ \theta^{\prime} \end{array}\right]=\left[\begin{array}{l} x \\ y \\ \theta \end{array}\right]+\left[\begin{array}{c} -\frac{v}{\omega} \sin (\theta)+\frac{v}{\omega} \sin \left(\theta+\omega_{t} \Delta t\right) \\ \frac{v}{\omega} \cos (\theta)-\frac{v}{\omega} \cos \left(\theta+\omega_{t} \Delta t\right) \\ \omega \Delta t \end{array}\right] \end{aligned}
  • Linearized the velocity motion model (對 prediction model 微分)
Ftx=∂f∂(x,y,θ)T[x′y′θ′]=[10−vtωtcos⁡(θ)+vtωtcos⁡(θ+ωtΔt)01−vtωtsin⁡(θ)+vtωtsin⁡(θ+ωtΔt)001]\begin{aligned} F_t^x = \frac{\partial f}{\partial(x,y,\theta)^T}\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ \theta^{\prime} \end{array}\right] = \left[\begin{array}{ccc} 1 & 0 & -\frac{v_{t}}{\omega_{t}} \cos (\theta)+\frac{v_{t}}{\omega_{t}} \cos \left(\theta+\omega_{t} \Delta t\right) \\ 0 & 1 & -\frac{v_{t}}{\omega_{t}} \sin (\theta)+\frac{v_{t}}{\omega_{t}} \sin \left(\theta+\omega_{t} \Delta t\right) \\ 0 & 0 & 1 \end{array}\right] \end{aligned}

Observation Model​

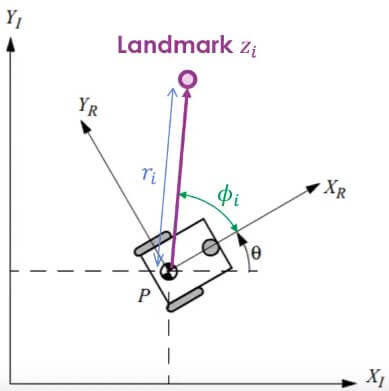EKF-SLAM observation model
EKF-SLAM observation model
  • Given observation model
zi=[qatan⁡2(δx,δy)−θ],δ=[mi,x−xmi,y−y],q=δTδ\begin{aligned} z_{i}=\left[\begin{array}{c} \sqrt{q} \\ \operatorname{atan} 2\left(\delta_{x}, \delta_{y}\right)-\theta \end{array}\right], \delta=\left[\begin{array}{c} m_{i, x}-x \\ m_{i, y}-y \end{array}\right], q=\delta^{T} \delta \end{aligned}
  • Linearized the observation model (對 observation model 微分)
Hi=∂zi∂(x,y,θ,mi,x,mi,y)=1q[−qδx−qδy0qδxqδyδy−δx−q−δyδx]\begin{aligned} H^{i}=\frac{\partial z_{i}}{\partial\left(x, y, \theta, m_{i, x}, m_{i, y}\right)}=\frac{1}{q}\left[\begin{array}{ccccc} -\sqrt{q} \delta_{x} & -\sqrt{q} \delta_{y} & 0 & \sqrt{q} \delta_{x} & \sqrt{q} \delta_{y} \\ \delta_{y} & -\delta_{x} & -q & -\delta_{y} & \delta_{x} \end{array}\right] \end{aligned}
  • 矩陣大小為 2 * 5
    • 2 為某個地標的 x, y 座標
    • 5 為自走車 pose 的 3 個變數 + 地標的 2 個座標 (x, y)
  • 如果今天觀察 l 個地標
    • 那矩陣大小就是 (2l) * (3 + 2l)

Summary​

我們可以建構關聯性的轉換矩陣，把上面兩種的局部結果，轉換到全局的整個狀態情況下

  • Prediction model (3*n, n 為狀態數量)
Ft=[1000⋯00100⋯00010⋯0]T×Ftx\begin{aligned} F_{t}=\left[\begin{array}{llllll} 1 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & \cdots & 0 \end{array}\right]^{T} \times F_{t}^{x} \end{aligned}
  • Observation model (5*n, 左上角 3 個與 pose 有關, 其餘每 2 個為 landmark)
Ht=[1000⋯0000⋯00100⋯0000⋯00010⋯0000⋯00000⋯0100⋯00000⋯0010⋯0]×Hti\begin{aligned} H_{t}=\left[\begin{array}{ccccccccccc} 1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \cdots & 0 & 1 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 0 & \cdots & 0 \end{array}\right] \times H_{t}^{i} \end{aligned}

有了全局的 Ft,HtF_{t}, H_{t} 就可以帶進 EKF 中開始計算

xkpre=f(xk−1est,uk)Pkpre=FkPk−1preFkT+QKk=PkpreHT(HPkpreHT+R)−1xkest=xkpre+Kk(zk−Hxkpre)Pkest=(I−KkH)Pkpre\begin{aligned} &x_{k}^{p r e}=f\left(x_{k-1}^{e s t}, u_{k}\right)\\ &P_{k}^{\text {pre}}={\color{red}F_{k}} P_{k-1}^{\text {pre}} {\color{red}F_{k}^{T}}+Q\\ &K_{k}=P_{k}^{p r e} {\color{red}H^{T}}\left({\color{red}H} P_{k}^{p r e} {\color{red}H^{T}}+R\right)^{-1}\\ &x_{k}^{e s t}=x_{k}^{p r e}+K_{k}\left(z_{k}-{\color{red}H} x_{k}^{p r e}\right)\\ &P_{k}^{e s t}=\left(I-K_{k} {\color{red}H}\right) P_{k}^{p r e} \end{aligned}