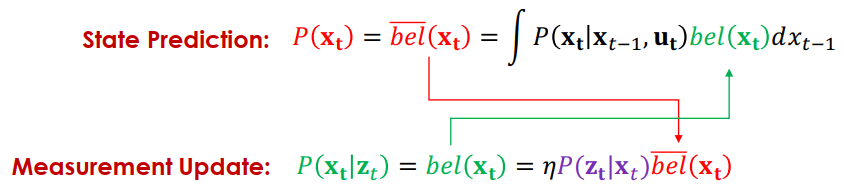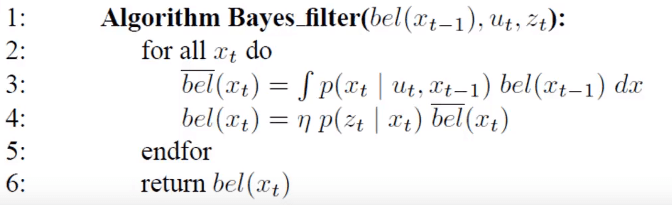SLAM Problem

SLAM (Simultaneous localization and mapping) 問題可以分為前端 (Prediction, Tracking, Mapping) 以及後端 (Filter-based, Graph-based)。SLAM 問題的目標是在不知道自己位置的情況下，能夠做到同時定位自己並且建構地圖。

Localization

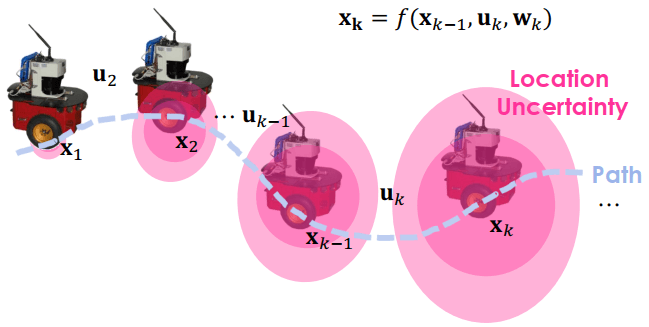
以下是自走車在不同時間 ($\mathbf{t}_k$) 移動到不同的位置 ($\mathbf{x}_k$)

• 自走車會透過控制指令 ($\mathbf{u}_k$) 進行移動
• 當中也會有一些誤差 ($\mathbf{w}_k$)

SLAM

所以我們可以把移動到新位置的公式寫作 $\mathbf{x}_k = f(\mathbf{x}_{k-1}, \mathbf{u}_k \mathbf{w}_k)$

• 下一個位置 ($\mathbf{x}_k$) 等於以下三者一起計算出來的
  • 前一個位置 ($\mathbf{x}_{k-1}$)
  • 控制指令 ($\mathbf{u}_k$)
  • 移動的 noise ($\mathbf{w}_k$)

Mapping

自走車行走中，同時也會用 sensor 來感測周圍的標的物 ($\mathbf{m}_j$)，計算測量值 ($\mathbf{z}_{k, j}$)

SLAM

在時間 k 測量目標 j 的結果可以寫成 $\mathbf{z}_{k, j} = h(\mathbf{m}_j, \mathbf{x}_k, \mathbf{v}_{k, j})$

• 在時間 k 對目標 j 測量的值 ($\mathbf{z}_{k, j}$) 等於以下三者所計算出來的
  • 目標物 ($\mathbf{m}_j$)
  • 車子位置 ($\mathbf{x}_k$)
  • 測量的 noise ($\mathbf{v}_{k, j}$)

Goal

可以看到 localize 和 mapping 都會有誤差，分別是 $\mathbf{w}_k$ 和 $\mathbf{v}_{k, j}$

• $\mathbf{w}_k$ 造成粉紅色的 location uncertainty
• $\mathbf{v}_{k, j}$ 造成藍色的 map uncertainty

而 SLAM 問題就是如何利用帶有這些 noise 的資料，也就是 $\mathbf{u}$ 和 $\mathbf{z}$，來估計自走車狀態 ($\mathbf{x}$)、和目標物狀態 ($\mathbf{m}$)

Probability Graphical Model for SLAM Problem

我們可以將 SLAM problem 轉為 probability graphical model 的樣式

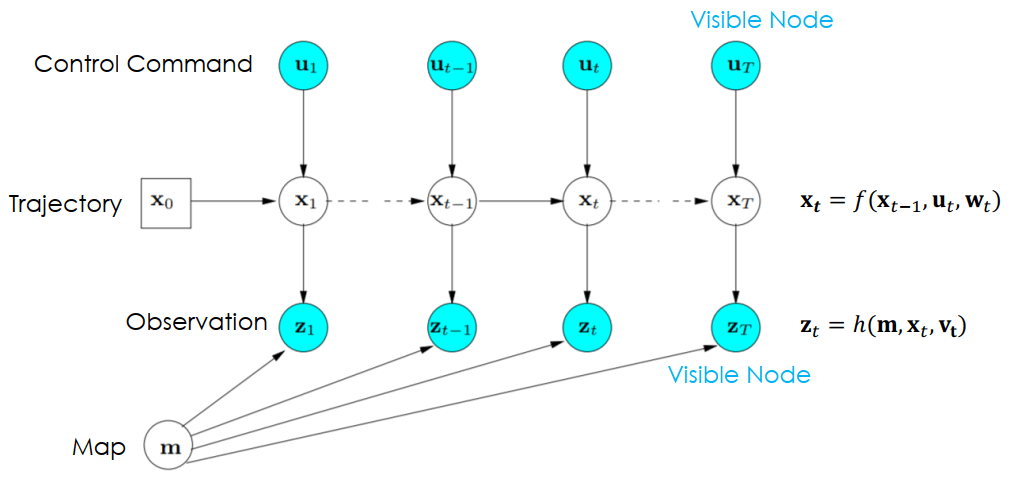SLAM Probability Graphical Model

• 每個變數變成了一個節點
• 藍色節點為 visible node 代表可以直接被偵測
• 箭頭代表了因果的關係
• Noise ($\mathbf{w}_t, \mathbf{v}_t$) 被自動 model 在這個機率模型裡面

可以看到在 SLAM problem 的兩個式子都可以在圖上被表現出來

$$\begin{aligned} &\mathbf{x}_{t}=f\left(\mathbf{x}_{t-1}, \mathbf{u}_{t}, \mathbf{w}_{t}\right)\\ &\mathbf{z}_{t}=h\left(\mathbf{m}, \mathbf{x}_{t}, \mathbf{v}_{\mathbf{t}}\right) \end{aligned}$$

Front-end

SLAM 有三個前端架構，結合在一起可以在特定時間 t 建立車子的位置 (pose, $\mathbf{x}_t$) 和環境的地圖 ($\mathbf{m}$)。若感測器為視覺感測器，那麼 front-end 又稱 visual odometry。

• Prediction
  • 從前一刻的 $\mathbf{x}_{t-1}$ 還有同時刻的 $\mathbf{u}_t$ 來推測該時刻的 $\mathbf{x}_t$

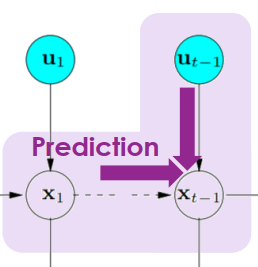SLAM Prediction

• Tracking
  • 根據目前觀測資訊 $\mathbf{z}_t$ 來推測目前的位置狀態 $\mathbf{x}_t$

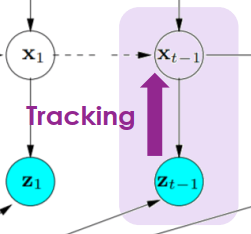SLAM Tracking

• Mapping
  • 根據目前觀測資訊 $\mathbf{z}_t$ 來建構地圖 $\mathbf{m}$

SLAM Mapping

Back-end

上面的觀測、預測通常會有誤差，累積後會產生錯誤，所以需要由 back-end 來修飾。在 back-end 有兩種做法來補償誤差，一種是 filter-based 一種是 graph-based。

• Filter-based error compensation
  • 直接根據最近的誤差來調整
  • 即時 (online) 但整體優化不佳

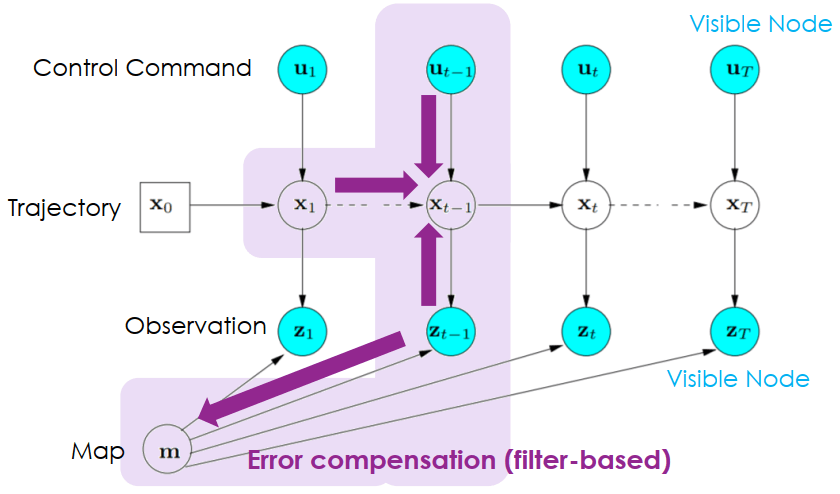SLAM Filter-based Error Compensation

• Graph-based error compensation
  • 每個時間點，都使用過去多個時間點的誤差來調整

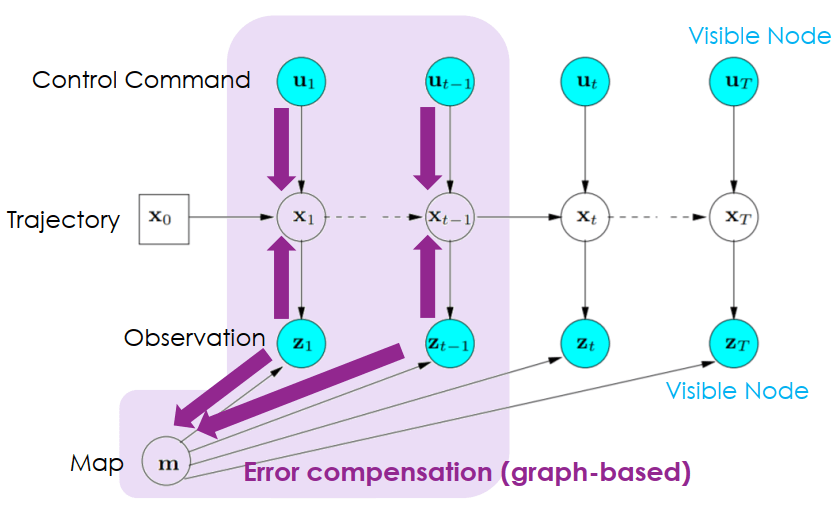SLAM Graph-based Error Compensation

發現 error 的方法稱為 loop closure detection

• 檢查自走車是否到達以前到過的位置
• 確定繞一圈後，將資訊丟給 error compensation

Probability Theory and Bayes Filter

Statistical Inference

Inference 是從 premises 來推測出 consequences 的過程，因為不可能從所有 premises 來推測，所以只拿一些 samples 來測，叫做 statistical inference。

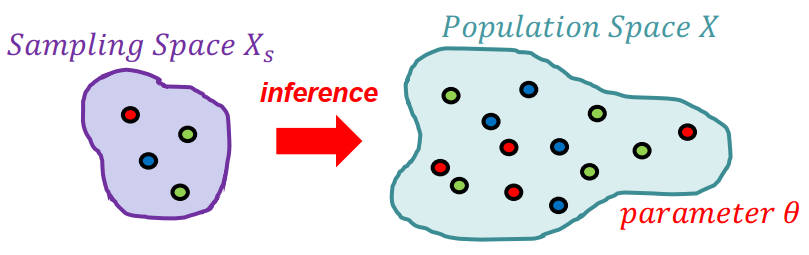Statistical Inference

• Hypothesis Testing (Top-down)
  • 是機器學習常用作法
  • 透過不斷假設 parameters 並帶入 samples 來評估結果是否正確
  • 最終得到最棒的 parameters
• Estimation (Bottom-up)
  • 直接從 samples 去推測 parameters

Maximum Likelihood Estimation

最有名的 estimation 是 MLE。MLE 看哪一個參數 ($\theta_k$) 的 likelihood 分布最有可能產生 samples ($x$)。

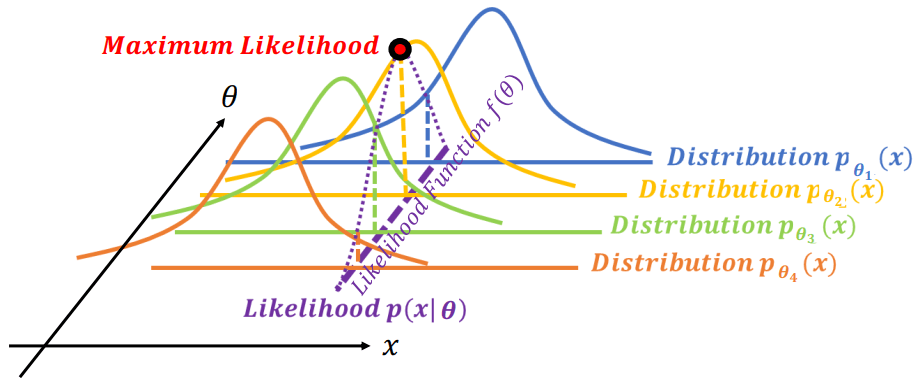Maximum Likelihood Estimation

可以看到在不同 $\theta$ 分布下產生 $x$ 的機率為 likelihood ($p(x\mid\theta)$)，而所有不同參數 $p(x\mid\theta)$ 所連成的線就是 likelihood function ($f(\theta)$)

Maximum a Posteriori Estimation

MLE 採樣時可能產生誤差，猜錯真正的 likelihood 分布，所以有了 MAP。MAP 多考量了 prior 的機率，所以可以降低 MLE 採樣錯誤所產生的誤差。

Maximum a Posteriori Estimation

Example

MLE

以投硬幣舉例，總共投了五次 (Tail, Tail, Tail, Head, Tail)，我們想知道正面機率 ($\theta$) 是多少，才造成上面的結果 ($x$)，也就是要求 likelihood ($p(x\mid\theta)$)。

$$\begin{aligned} &\text{Find } \max _{p} \theta(1-\theta)^{4}\\\\ &\frac{d \theta(1-\theta)^{4}}{d \theta}=(1-\theta)^{4}+4 \theta(1-\theta)^{3}(-1)=(1-\theta)^{3}(5 \theta-1)=0\\\\ &\theta = 0.2 \end{aligned}$$

MAP

同樣的題目，我們定義 prior 為 Discrete Uniform Distribution，也就是各為 1/11 (0.0 到 1.0)

$\frac{p(\theta) p(x | \theta)}{p(x)}=p(\theta | x)$

$$\begin{aligned} \frac{\begin{bmatrix} 1/11 \\ 1/11 \\ 1/11 \\\vdots \end{bmatrix} \times \begin{bmatrix} (0)^1(1)^4 \\ (0.1)^1(0.9)^4 \\ (0.2)^1(0.8)^4 \\\vdots \end{bmatrix} }{p(x) = \sum_\theta p(x, \theta) = \sum_\theta p(x\mid\theta)p(\theta)} = \begin{bmatrix} 0.000\\0.213\\0.333\\\vdots \end{bmatrix} \end{aligned}$$

因為 prior 是 uniform distribution，所以其實 MAP 沒有改變太多

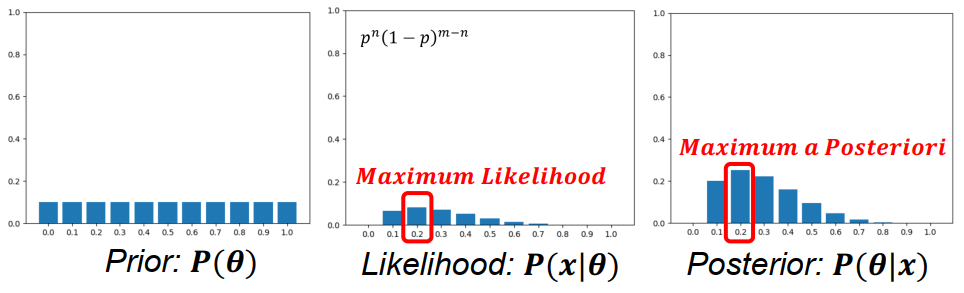MLE vs MAP

Bayesian Approach

不斷用 prior + likelihood 來計算 posterior 並更新假設

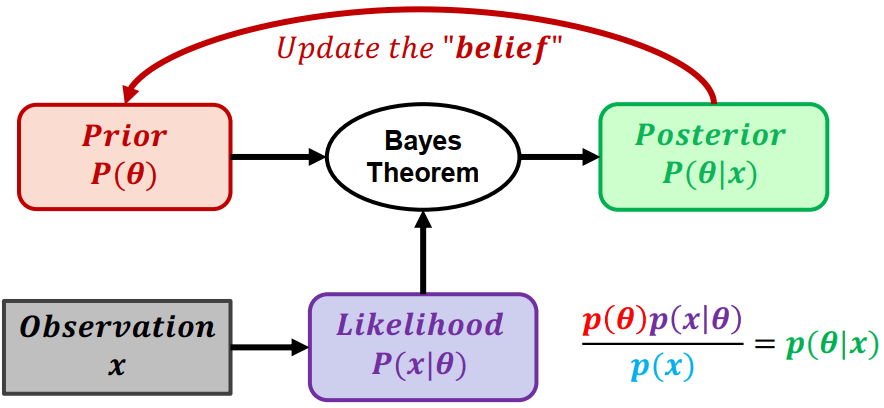Bayesian Approach

不再是看誰讓 likelihood 或 posterior 最大化，而是直接觀察 parameters 的分布

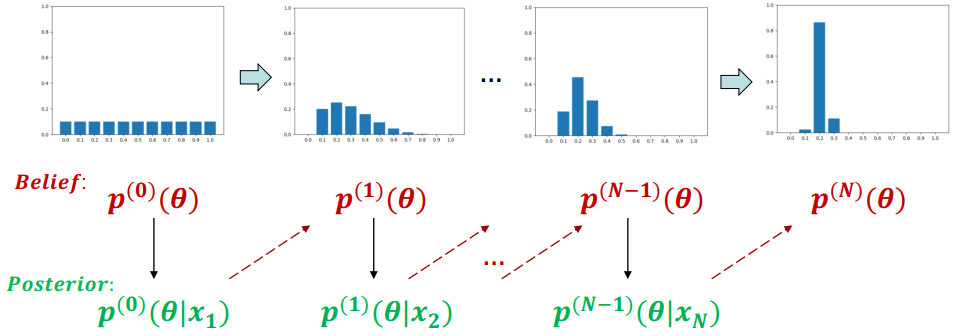Bayesian Approach Example

Bayes Filter

Bayesian approach 會將參數 ($\theta$) 帶入 prior、likelihood 計算出 posterior。posterior 再重新做為下一輪的 belief 進行計算，最終找出參數 ($\theta$) 的分布

State Prediction

我們也可以應用於 SLAM 的 probability graphical model

$$\begin{aligned} P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) &=\int P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{x}_{t-1}, \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) \mathrm{P}\left(\mathbf{x}_{t-1} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) d x_{t-1} \\ &=\int P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{x}_{t-1}, \mathbf{u}_{t}\right) \mathrm{P}\left(\mathbf{x}_{t-1} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) d x_{t-1} \end{aligned}$$

• 我們可以用 $\mathbf{u}_1$ 到 $\mathbf{u}_t$
• 以及 $\mathbf{z}_1$ 到 $\mathbf{z}_t$
• 來估算當前時間點的 $\mathbf{x}_t$

備註

化簡中，因為 $\mathbf{x}_{t-1}$ 為已知，所以 $\mathbf{x}_{t-1}$ 之前的觀測資訊就都不重要了。

我們可以將式子簡寫成以下樣子 (bel 代表 belief)

$$\overline{b e l}\left(\mathbf{x}_{\mathrm{t}}\right)=\int P\left(\mathbf{x}_{\mathrm{t}} \mid \mathbf{x}_{t-1}, \mathbf{u}_{t}\right) b e l\left(\mathbf{x}_{\mathrm{t}}\right) d x_{t-1}$$

• $\overline{b e l}\left(\mathbf{x}_{\mathrm{t}}\right)$ 為當下時刻的估測
  • 當下時刻還沒觀測到同時間的 $\mathbf{z}_t$
• $b e l\left(\mathbf{x}_{\mathrm{t}}\right)$ 為前一時刻的估測
  • 已經觀測到該時間點的 $\mathbf{t}_{t-1}$

Measurement Update

當我們得到了觀測資訊 ($\mathbf{z}_t$) 就可以用來更新位置資訊 ($\mathbf{x}_t$)

$$\begin{aligned} P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{z}_{1: t}, \mathbf{u}_{1: t}\right) &=\frac{P\left(\mathbf{z}_{\mathrm{t}} | \mathbf{x}_{\mathrm{t}}, \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right)}{P\left(\mathbf{z}_{\mathrm{t}} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right)} \\ &=\eta P\left(\mathbf{z}_{\mathrm{t}} | \mathbf{x}_{\mathrm{t}}, \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) \\ &=\eta P\left(\mathbf{z}_{\mathrm{t}} | \mathbf{x}_{\mathrm{t}}\right) P\left(\mathbf{x}_{\mathrm{t}} | \mathbf{z}_{1: t-1}, \mathbf{u}_{1: t}\right) \\ \end{aligned}$$

• 可以看到左邊的算式中有 $\mathbf{z}_{1:t}$
• 但右邊的只有 $\mathbf{z}_{1:t-1}$

一樣可以轉成以下的 belief 表達方式

$$b e l\left(\mathbf{x}_{\mathrm{t}}\right)=\eta P\left(\mathbf{z}_{\mathrm{t}} | \mathbf{x}_{t}\right) \overline{b e l}\left(\mathbf{x}_{\mathrm{t}}\right)$$

• $bel$ 表示有 $\mathbf{z}_t$ 資訊
• $\overline{bel}$ 表示沒有 $\mathbf{z}_t$ 資訊

Bayes Filter Algorithm

Bayes filter 就是上面兩個式子遞迴互相更新所產生

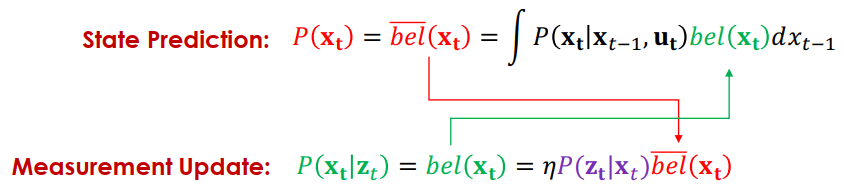Bayes Filter Algorithm

寫成 pseudo code 表示為

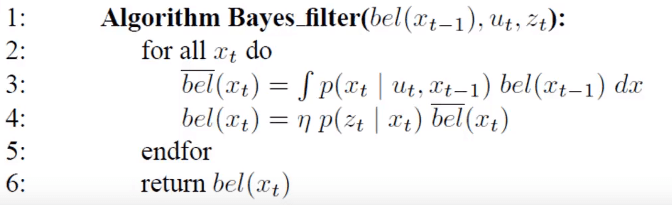Bayes Filter Algorithm Pseudo Code

Example

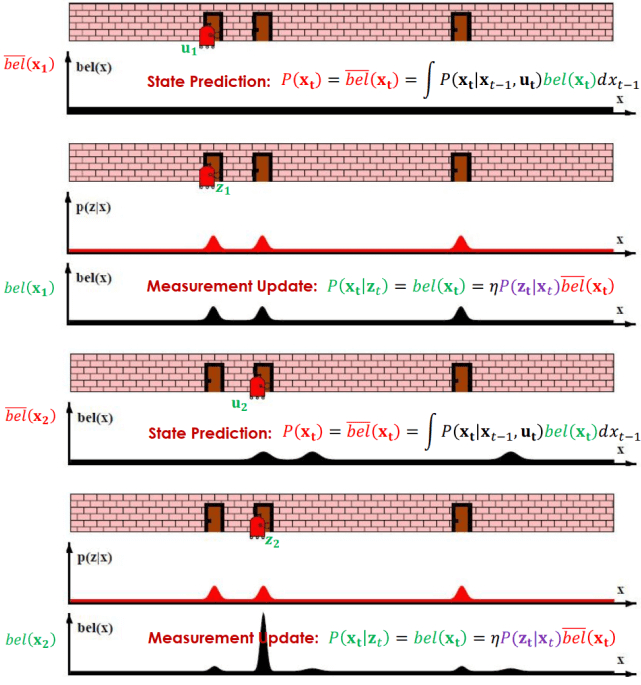Bayes Filter Algorithm Example

• 一開始的 $bel(\mathbf{x}_t)$ 是 prior distribution
• 感測到 $\mathbf{z}_1$ 得到 likelihood ($P(\mathbf{z}_t\mid\mathbf{x}_t)$) 後可以更新 $bel(\mathbf{x}_1)$
• 接著有了 $\mathbf{u}_2$ 可以更新運動狀態 $\overline{bel}(\mathbf{x}_2)$
• 接著一樣感測到 $\mathbf{z}_2$ 更新回去得到最新的 $bel(\mathbf{x}_2)$