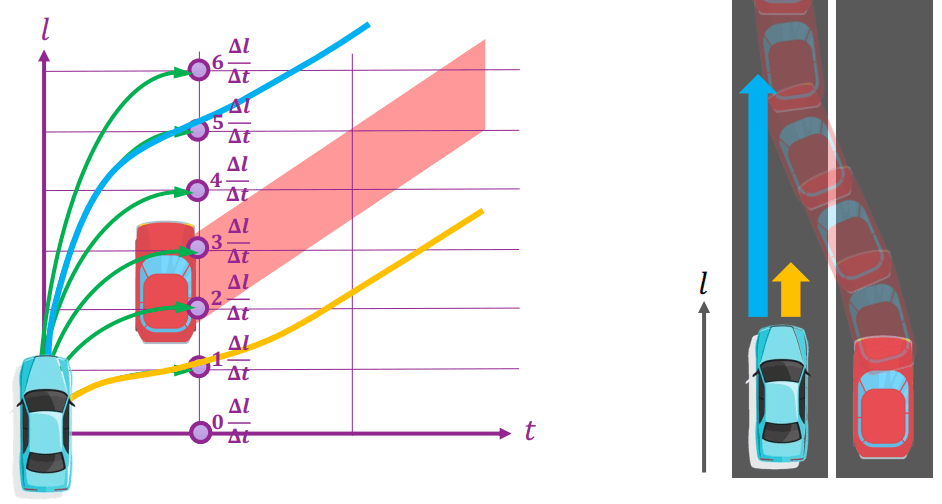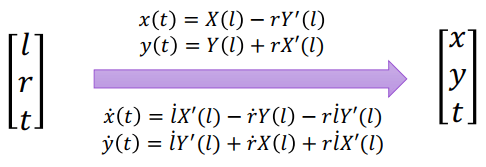本文將描述如何使用 State lattice planning 和 Frenet Coordinate 來計算自駕車的軌跡。State lattice planning 透過結合空間和時間,採樣軌跡並計算成本,再檢查軌跡是否可用,並選擇成本最低的軌跡。Frenet Coordinate 將車子位置投影到二維路徑,求取一階、二階微分和最低成本。最後,Trajectory Planning 考慮動態障礙物,計算每個時間點的運動資訊,找出最低成本的軌跡。
一般的自走車,不需要考慮環境變化,只需要預測障礙與終點規劃,所以可以使用 nontemporal state lattice 來規劃曲線。
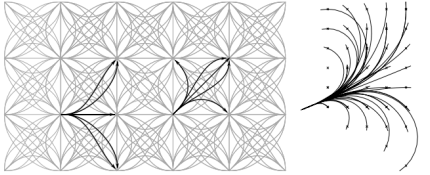 Lattices Planning
Lattices Planning自駕車則需要考慮的周遭動態的變化,所以有人發明了結合 temporal 和 spatial 的規劃方法
 State Lattices Planning
State Lattices Planning這就是 State lattice planning
- 在結合的空間及時間中,採樣軌跡
- 計算每條軌跡的代價
- 代價可以有很多種
- Objective achievement cost (目標與終點距離)
- Lateral offset cost (遵守交通規則)
- Collision cost (避免碰撞)
- Longitude jerk cost (舒服)
- Lateral acceleration cost (舒服)
- 確認軌跡是否能夠使用 (有無避障),並選擇最低代價的那條軌跡
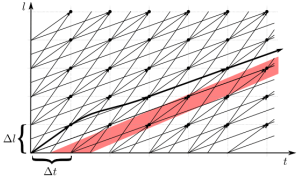
下圖是一個一維道路的 spatiotemporal state lattice
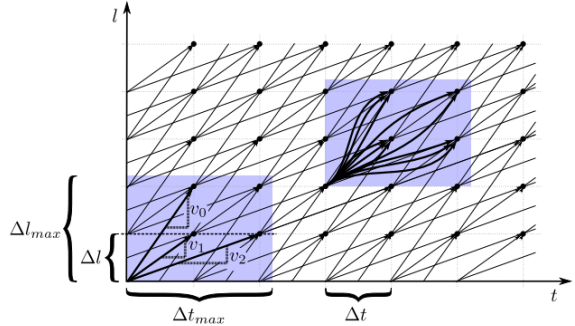 Spatiotemporal State Lattices
Spatiotemporal State Lattices- l: 代表空間
- t: 代表時間
- Δl,Δt: 代表空間和時間的 resolution
- Δlmax,Δtmax: 代表空間和時間的 constraints
其中線段的斜率代表了縱向的速度,例如 v0 線段的速度為 2,而 v1 線段的速度為 1。右上的藍色限制區塊,展示了套用平滑的規劃曲線結果。
假設紅色車子想要超越藍色車子,我們可以將所有條件投射到 spatiotemporal state lattice
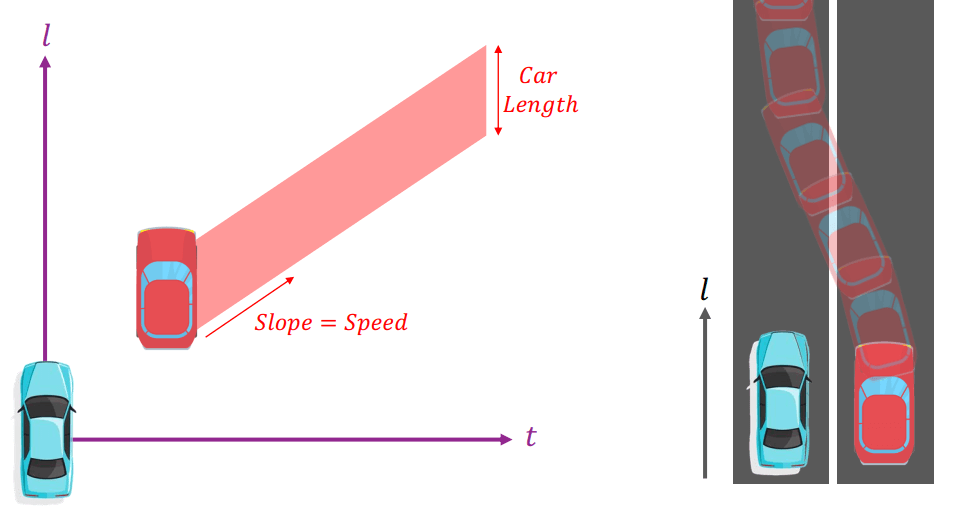 Spatiotemporal State Lattices
Spatiotemporal State Lattices讓我們可以直接在 lattice 上進行規劃
- 平形四邊形的寬度: 紅色車子長度
- 平形四邊形的斜率: 紅色車子速度
藍色車子可以選擇加速或減速,所以代表在 lattice 上的某個時間點,可以有好幾種不同的速度選擇
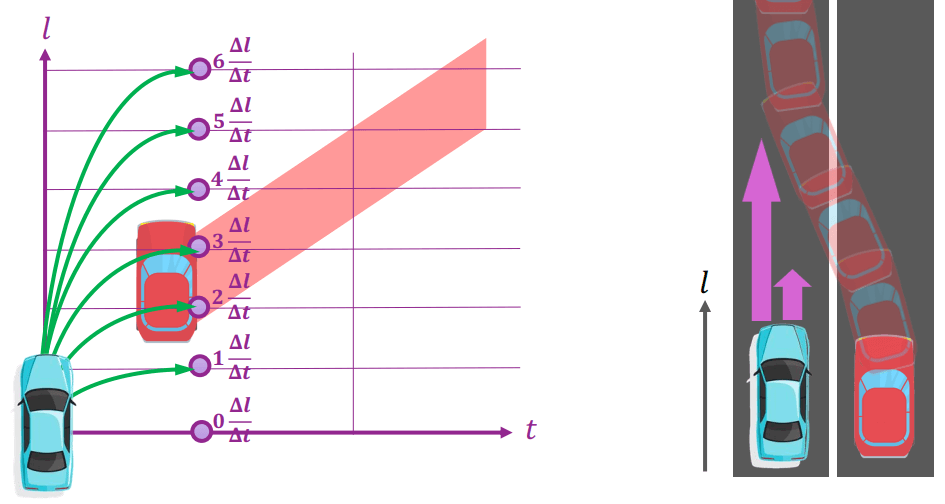 Spatiotemporal State Lattices
Spatiotemporal State Lattices我們對這些採樣進行平滑計算並處理,得到了加速或減速各別最佳 (最小 cost) 的結果
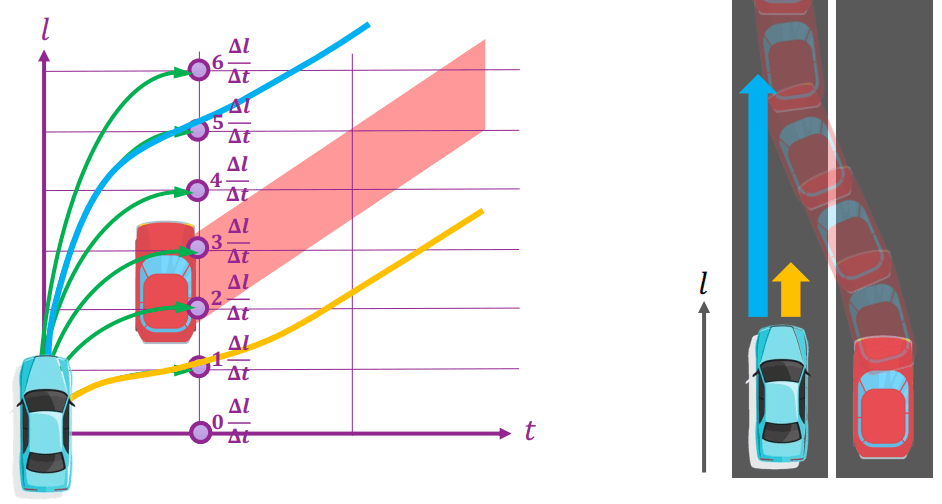 Spatiotemporal State Lattices
Spatiotemporal State Lattices所以藍色線段會選擇超車,而黃色線段會選擇跟車
看完一維空間後,再來要考慮蜿蜒的二維空間
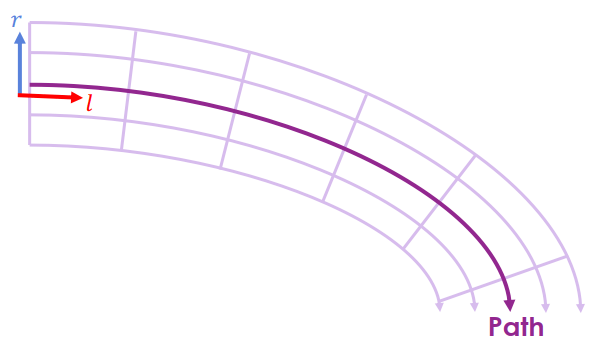 Frenet Coordinate
Frenet CoordinateFrenet coordinate 將車子位置投影到二維路徑中
- l: 代表路徑方向的位移
- r: 代表與路徑的橫向誤差
我們的目標是從路徑點和參數,計算出該參數之下的座標點
- 路徑點: (Xs(l),Ys(l))
- 參數: (l,r)
- 目標座標: (x(t),y(t))
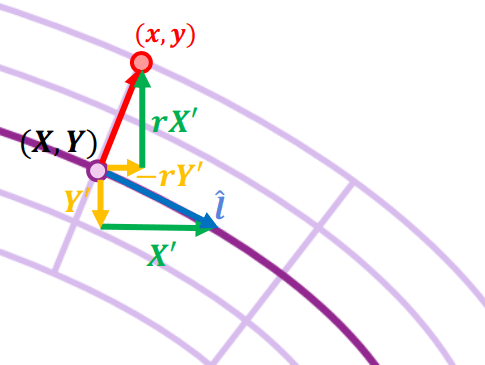 Frenet Coordinate
Frenet Coordinate從圖形中可以推出以下公式 (轉換方程: Frenet to standard coordinate)
x(t)=X(l)−rY′(l)y(t)=Y(l)+rX′(l) 我們可以進一步對轉換方程,求取其一階、二階微分
x˙(t)=l˙X′(l)−r˙Y(l)−rl˙Y′(l)y˙(t)=l˙Y′(l)+r˙X(l)+rl˙X′(l)x¨(t)=l¨X′+l¨2X′′−r¨Y−(2r˙l˙+rl¨)Y′−r˙l˙2Y′′y¨(t)=l¨Y′+l¨2Y′′−r¨X−(2r˙l˙+rl¨)X′−r˙l˙2X′′ 現在我們來生成二維的軌跡,定義車子狀態、縱向狀態、橫向狀態
Vehicle States
- [x,y,θ,v,a]
Longitude States
- l: longitude distance
- l˙: longitude speed
- l¨: longitude acceleration
Lateral States
- r: lateral offset
- r˙: lateral speed
- r¨: lateral acceleration
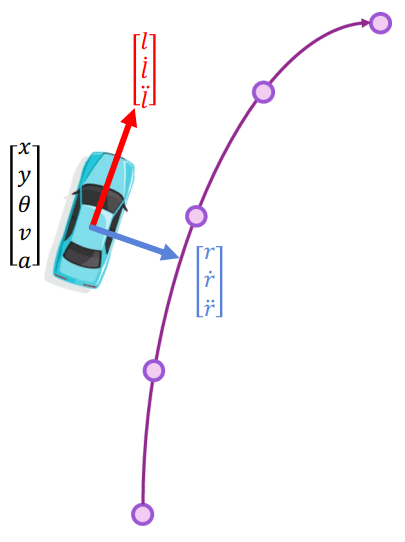 Trajectory Generation
Trajectory Generation分別定義起始時 (t0) 的狀態,還有終點時 (t1) 的狀態
State at time t0:{(r0,r˙0,r¨0),(l0,l˙0,l¨0)}State at time t1:{(r1,r˙1,r¨1),(l1,l˙1,l¨1)} 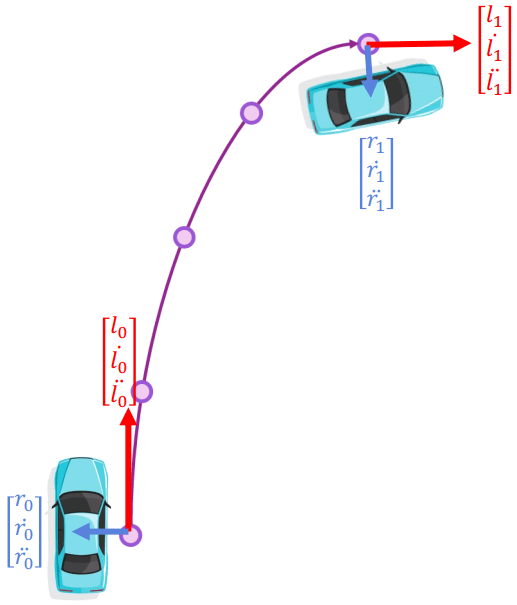 Trajectory Generation
Trajectory Generation將開始與結束作為 curve function 的 boundary condition
- 符合 longitude trajectory (l(t)) 的 boundary condition
l(t0)=l0,l(t1)=l1l˙(t0)=l˙0,l˙(t1)=l˙1l¨(t0)=l¨0,l¨(t1)=l¨1 - 符合 lateral trajectory (r(t)) 的 boundary condition
r(t0)=r0,r(t1)=r1r˙(t0)=r˙0,r˙(t1)=r˙1r¨(t0)=r¨0,r¨(t1)=r¨1 最終我們就可以將任意時間點 t 帶入 curve function 求得 longitude 和 lateral 的值: l=l(t),r=r(t)。 接著就可以用剛剛在 Frenet 推導的公式,將這些在 Frenet 的狀態轉換到標準座標系上得到目標軌跡。
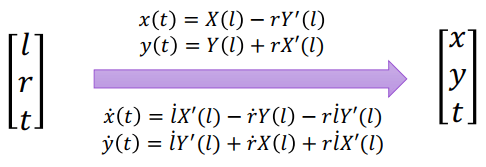 Frenet to Standard
Frenet to Standard以下是一個在二維情況下,進行軌跡規劃的結果
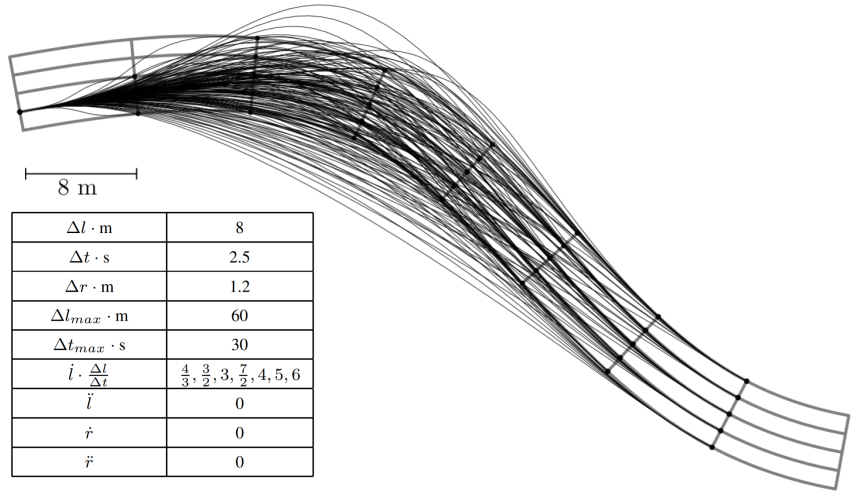 Trajectory Planning Example
Trajectory Planning Example