跳至主要内容

Curve Interpolation II

本文探討了三種不同的曲線插值技術，分別是 Hermite Curves、Bezier Curves 和 Cubic B-spline Curves，它們都可以使用控制點來產生出曲線，但本文突出了 Cubic B-spline Curves 的優點，它可以讓兩個區段在接點處，一階微分的值是相同的，甚至可以滿足接點處的二階微分也相同，為了更加平滑的曲線。

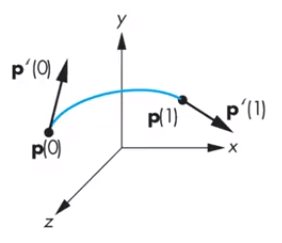
Hermite Curves​

Hermite curves 是另一種使用 control points 產生出 curve 的方式，特別的是，只需透過頭和尾兩個點的位置及一階微分資訊來求得

Hermite curves
Hermite curves
  • 我們先知道 P 的一階微分長怎樣
p(u)=c0+c1u+c2u2+c3u3p′(u)=c1+2uc2+3u2c3\begin{aligned} &\mathbf{p}(u)=c_{0}+c_{1} u+c_{2} u^{2}+c_{3} u^{3}\\ &\mathbf{p}^{\prime}(u)=\mathbf{c}_{1}+2 u \mathbf{c}_{2}+3 u^{2} \mathbf{c}_{3} \end{aligned}
  • 位置
p0=p(0)=c0p3=p(1)=c0+c1+c2+c3\begin{aligned} &\mathbf{p}_{0}=\mathbf{p}(0)=\mathbf{c}_{0}\\ &\mathbf{p}_{3}=\mathbf{p}(\mathbf{1})=\mathbf{c}_{0}+\mathbf{c}_{1}+\mathbf{c}_{2}+\mathbf{c}_{3} \end{aligned}
  • 一階微分
p0′=p′(0)=c1p3′=p′(1)=c1+2c2+3c3\begin{aligned} &\mathbf{p}_{0}^{\prime}=\mathbf{p}^{\prime}(0)=\mathbf{c}_{1}\\ &\mathbf{p}_{3}^{\prime}=\mathbf{p}^{\prime}(\mathbf{1})=\mathbf{c}_{1}+2 \mathbf{c}_{2}+3 \mathbf{c}_{3} \end{aligned}

我們一樣可以得到 Q=Ac\mathbf{Q}=\mathbf{A c}，其中的 A−1\mathbf{A}^{-1} 可以記為 MH\mathbf{M}_{\mathbf{H}} (Hermite Geometry Matrix)

Q=[p0p3p0′p3′]=[1000111101000123]c,MH=[1000111101000123]−1=[10000010−33−2−12211]\begin{aligned} \mathbf{Q}=\left[\begin{array}{l} \mathbf{p}_{0} \\ \mathbf{p}_{3} \\ \mathbf{p}_{0}^{\prime} \\ \mathbf{p}_{3}^{\prime} \end{array}\right]=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 3 \end{array}\right] \mathbf{c}, \quad \mathbf{M}_{\mathbf{H}}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 3 \end{array}\right]^{-1}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -3 & 3 & -2 & -1 \\ 2 & 2 & 1 & 1 \end{array}\right] \end{aligned}

再來就可以算出 c\mathbf{c} 矩陣，進而得到 p(u)\mathbf{p}(u)

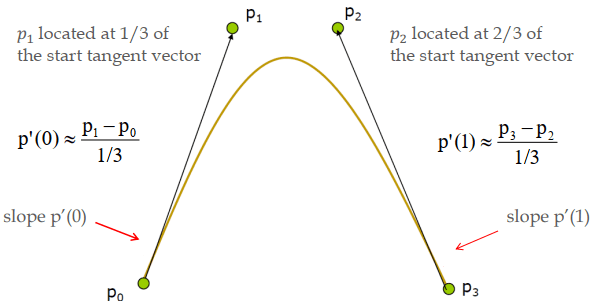
c=MHQp(u)=uTc=uTMHQ\begin{aligned} &\mathbf{c}=\mathbf{M}_{\mathbf{H}} \mathbf{Q}\\ &\mathbf{p}(u)=\mathbf{u}^{T} \mathbf{c}=\mathbf{u}^{T} \mathbf{M}_{H} \mathbf{Q} \end{aligned}

Bezier Curves​

當我們只知道四個 control points 而不知道任何的一階微分資訊時，就可以使用 bezier curves，他可以利用 p1, p2 的位置，來預估頭尾 p0, p3 的一階微分

Bezier curves
Bezier curves
備註

1/3 是兩點的間距

所以 Bezier 跟 Hermite 只差在一階微分的值，是用近似的方法求得

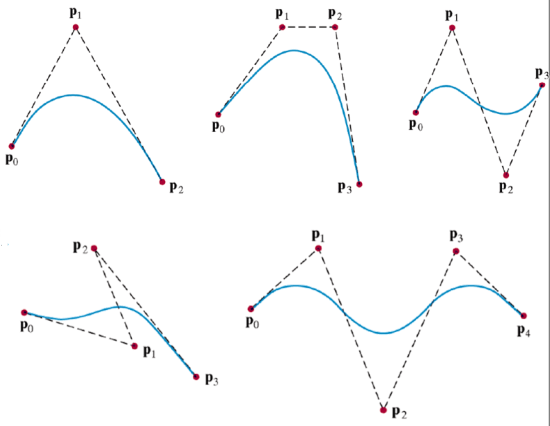
P(0)=P0=c0P(1)=P3=c0+c1+c2+c3P′(0)=3(P1−P0)=c1P′(1)=3(P3−P2)=c1+2c2+3c3c=MBP,MB=[1000−33003−630−13−31]p(u)=uTc=uTMBP\begin{aligned} &P(0)=P_{0}=c_{0}\\ &P(1)=P_{3}=c_{0}+c_{1}+c_{2}+c_{3}\\\\ &P^{\prime}(0)=3\left(P_{1}-P_{0}\right)=c_{1}\\ &P^{\prime}(1)=3\left(P_{3}-P_{2}\right)=c_{1}+2 c_{2}+3 c_{3}\\\\ &\mathbf{c}=\mathbf{M}_{\mathrm{B}} \mathbf{P}, \quad \mathbf{M}_{\mathrm{B}}=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ -3 & 3 & 0 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1\end{array}\right]\\ &\mathbf{p}(u)=\mathbf{u}^{T} \mathbf{c}=\mathbf{u}^{T} \mathbf{M}_{\mathrm{B}} \mathbf{P} \end{aligned}

從以下五個 bezier curves 可以看到，中間點皆是為了預測頭尾微分，而非真正要連接的點

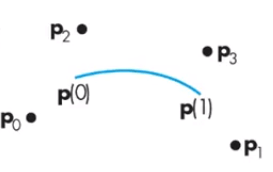
Bezier curves example
Bezier curves example

Cubic B-spline Curves​

上述所產生的 local curves 在連接時，依然會有一階微分不同導致不平滑的問題，解決方法是透過 B-spline curves

  • 讓 curves 不一定要通過頭尾的 control points
  • 但卻可以讓兩個區段在接點處，一階微分的值是相同的
  • 事實上 B-spline 還能滿足接點處的二階微分相同
B-spline curves
B-spline curves

在推導時，一樣是每四個 control points 來求得一個 curve

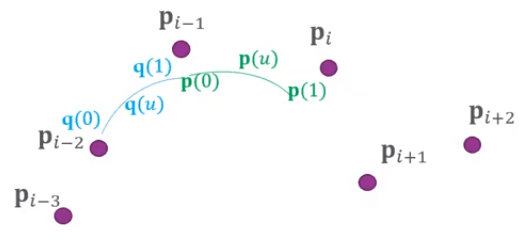
B-spline curves continuity
B-spline curves continuity
  • q(u)q(u) 由 pi−3,pi−2,pi−1,pi\mathbf{p}_{i-3}, \mathbf{p}_{i-2}, \mathbf{p}_{i-1}, \mathbf{p}_{i} 推導而出
  • p(u)p(u) 由 pi−2,pi−1,pi,pi+1,\mathbf{p}_{i-2}, \mathbf{p}_{i-1}, \mathbf{p}_{i}, \mathbf{p}_{i+1}, 推導而出

我們希望這兩個區段的 q(1)q(1) 和 p(0)p(0) 的位置相同、一階微分也相同，所以要滿足以下式子

p(0)=q(1)=16(pi−2+4pi−1+pi)p′(0)=q′(1)=12(pi−pi−2)\begin{aligned} &\mathbf{p}(0)=\mathbf{q}(1)= \color{red}{\frac{1}{6}\left(\mathbf{p}_{i-2}+4 \mathbf{p}_{i-1}+\mathbf{p}_{i}\right)}\\ &\mathbf{p}^{\prime}(0)=\mathbf{q}^{\prime}(1)= \color{red}{\frac{1}{2}\left(\mathbf{p}_{i}-\mathbf{p}_{i-2}\right)} \end{aligned}

後方求值的設定 (紅色處) 不是固定的，以上只是列出常用的做法

  • 位置使用鄰近的三個 points 來預估
  • 一階微分則用鄰近的兩個 points 來預估
  • 要注意鄰近的點需要從兩個區段都有用到的點才能拿來使用
Since p(u)=c0+c1u+c2u2+c3u3=uTcp(0)=c0=16(pi−2+4pi−1+pi)p′(0)=c1=12(pi−pi−2)p(1)=c0+c1+c2+c3=16(pi−1+4pi+pi+1)p′(1)=c1+2c2+3c3=12(pi+1−pi−1)\begin{aligned} \text{Since } &\mathbf{p}(u)=\mathbf{c}_{0}+\mathbf{c}_{1} u+\mathbf{c}_{2} u^{2}+\mathbf{c}_{3} u^{3}=u^{T} \mathbf{c}\\ &\mathbf{p}(0)=\mathbf{c}_{0}=\frac{1}{6}\left(\mathbf{p}_{i-2}+4 \mathbf{p}_{i-1}+\mathbf{p}_{i}\right) \\ &\mathbf{p}^{\prime}(0)=\mathbf{c}_{1}=\frac{1}{2}\left(\mathbf{p}_{i}-\mathbf{p}_{i-2}\right) \\ &\mathbf{p}(1)=\mathbf{c}_{0}+\mathbf{c}_{1}+\mathbf{c}_{2}+\mathbf{c}_{3}=\frac{1}{6}\left(\mathbf{p}_{i-1}+4 \mathbf{p}_{i}+\mathbf{p}_{i+1}\right) \\ &\mathbf{p}^{\prime}(1)=\mathbf{c}_{1}+2 \mathbf{c}_{2}+3 \mathbf{c}_{3}=\frac{1}{2}\left(\mathbf{p}_{i+1}-\mathbf{p}_{i-1}\right) \end{aligned}

最後我們就可以像其他兩種 curves 一樣推導出 c\mathbf{c} 和 p(u)\mathbf{p}(u)

P=AcMS=A−1=16[1410−30303−630−13−31]⇒c=MSP⇒p(u)=uTc=uTMSP\begin{aligned} &\mathbf{P}=\mathbf{A c}\\ &\mathbf{M}_{\mathrm{S}}=\mathbf{A}^{-1}=\frac{1}{6}\left[\begin{array}{cccc} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{array}\right] &&\Rightarrow \mathbf{c}=\mathbf{M}_{\mathrm{S}} \mathbf{P}\\ & \quad&&\Rightarrow \mathbf{p}(u)=u^{T} \mathbf{c} = u^T\mathbf{M}_{\mathrm{S}} \mathbf{P} \end{aligned}