跳至主要内容

Introduction

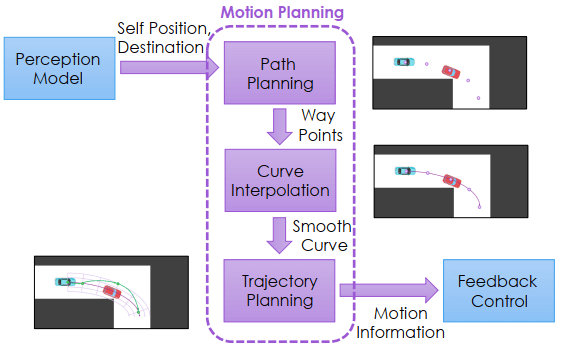
Motion planning 是一種解決移動問題的技術，它志在找出一連串動作序列，讓車子移動到終點，要求動作序列需要避免撞到障礙物、動作限制（如最大速度等）、移動路徑需要平滑以及最短路徑。Motion planning 可以分成三部分：Path Planning、Curve Interpolation 和 Trajectory Planning。

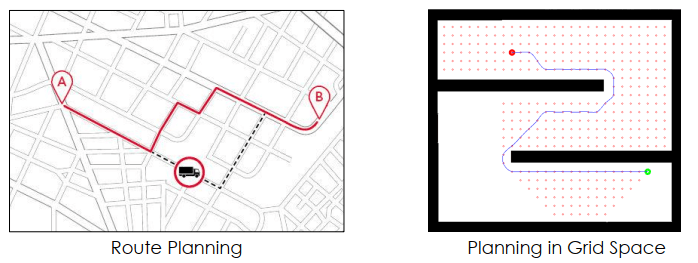
Path Planning 將地圖轉換成交叉點口或離散網格節點，Curve Interpolation 則是用一個曲線函數連接節點，使得路徑變得平滑，Trajectory Planning 則是考慮動態障礙物，並計算出每個時間點的運動資訊，找出 cost 最小的當作合適的軌跡。

Introduction to Motion Planning​

Motion planning 志在找出一連串動作序列，讓車子移動到終點，動作序列必須要滿足一些要求:

  • 避免撞到障礙物
  • 動作限制 (e.g., maximum speed)
  • 移動路徑需要平滑
  • 最短路徑

Motion planning 可以分成三部分:

  • Path planning
  • Curve interpolation
  • Trajectory planning

Path Planning​

Path planning
Path planning

地圖可以被轉換成以上兩種格式:

  1. 交叉點口做為節點
  2. 產生離散網格，每一點做為節點

這些節點稱為 weight points，用來做為 shortest path algorithm 的單位

Path planning
Path planning

問題有三:

  1. 節點分配不均
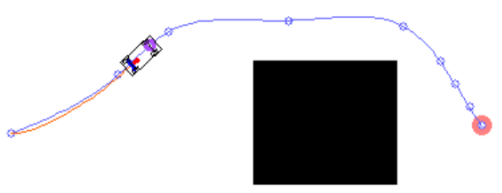
  2. 形成路徑不夠平滑
  3. 節點資訊不夠 (一階、二階微分資訊)

Curve Interpolation​

Curve interpolation
Curve interpolation

用一個 curve function 來連接 weight points 使得路徑變得平滑，並讓路徑點獲得微分資訊。

Trajectory Planning​

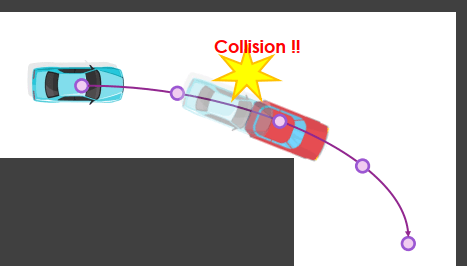
在動態中可能有移動的物體成為障礙物

Dynamic environment problem
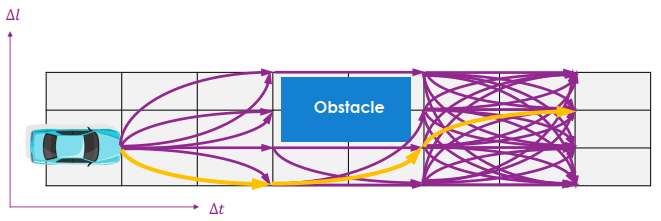
Dynamic environment problem

Trajectory planning 除了規劃路徑外，還要計算出每個時間點的運動資訊，根據預測 obstacle 的未來行動來規劃每個時間點的動作

Trajectory planning
Trajectory planning
  • y-axis 為車子的位移
  • x-axis 為時間

所以會在離散時間點，進行路徑的採樣，找出當中 cost 最小的當作合適的軌跡

Motion Planning Flow​

Motion planning flow
Motion planning flow

整個 motion planning 的流程如圖所示

  1. 路徑規劃: 得到空間節點
  2. 內插: 得到較平滑的曲線、微分資訊
  3. 軌跡規劃: 得到運動狀態、時間規劃
  4. 運用前一章所講的 feedback control 來移動車子

Path vs. Trajectory​

Motion planning = Path planning + Trajectory planning

  • Path planning (只考慮空間資訊)
Input: Start/End Position{[xs,ys],[xe,ye]}Output: Way Points{[xs,ys],[x1,y1],[x2,y2],…,[xe,ye]}\begin{aligned} &\text{Input: Start/End Position} \left\{\left[x_{s}, y_{s}\right],\left[x_{e}, y_{e}\right]\right\} \\ &\text{Output: Way Points} \left\{\left[x_{s}, y_{s}\right],\left[x_{1}, y_{1}\right],\left[x_{2}, y_{2}\right], \ldots,\left[x_{e}, y_{e}\right]\right\} \end{aligned}
  • Trajectory planning (考慮空間及時間資訊)
Inputs: Start/End Position{[xs,ys],[xe,ye]}Curve Functionf(x).Time DensityΔtOutputs: Motion information with time{[x0,y0,v0,a0,t0],[x1,y1,v1,a1,t1],[x2,y2,v2,a2,t2],…,[xN,yN,vN,aN,tN]}\begin{aligned} \text{Inputs: } &\text{Start/End Position} \left\{\left[x_{s}, y_{s}\right],\left[x_{e}, y_{e}\right]\right\} \\ &\text{Curve Function} f(x). \\ &\text{Time Density} \Delta t \\\\ \text{Outputs: } &\text{Motion information with time} \\ &\left\{\left[x_{0}, y_{0}, v_{0}, a_{0}, t_{0}\right],\left[x_{1}, y_{1}, v_{1}, a_{1}, t_{1}\right],\left[x_{2}, y_{2}, v_{2}, a_{2}, t_{2}\right], \ldots,\left[x_{N}, y_{N}, v_{N}, a_{N}, t_{N}\right]\right\} \end{aligned}