Path Planning
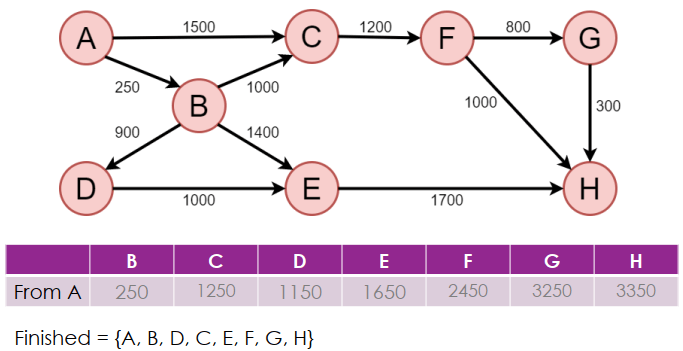
本文介紹 Path Planning,它是為了讓機器人知道如何從一個起點到達另一個終點的策略。它讓我們可以用 Graph G 來表示地圖,其中 G = (V, E),V 是一組點,E 是一組邊。而另外也會有 weights 來求解 single-source shortest path,即給定起點的最短路徑。
我們會介紹三種算法,Dijkstra 、Best-First Search (BFS) 以及 A*,同時也會提到 Heuristic function 以及 Sampling Based Planning Methods。PRM 和 RRT 是兩種 sampling based planning 的方法,而 RRT* 是 RRT 的改良版本。
在 Path planning 要先把地圖轉換成 graph G
- G = (V, E)
- V: a set of Vertices
- E: a set of Edges
在 edges 上可能有 weights,我們就可以求解 single-source shortest path (給定起點的最短路徑)
- Dijkstra: 用來求 non-negative weights graph
- Best-First Search (BFS): 是一種 heuristic greedy search
- A*: BFS + Dijkstra
Dijkstra's Algorithm
Dijkstra 可以找到最佳路徑,但不能有負的 weights
從一個 start point (v)
- 找出距離最短且還沒結束的 vertex (u)
- 更新其他沒結束的 vertex (v')
- d(v, v’) = min(d(v, u) + <u, v’>, d(v, v’))
Pseudo code
def Dijkstra(G, weight, v_start):
for each vertex v in G.vertices:
v.distance = INF
v.predecessor = None
v_start.distance = 0
Q = set(G.vertices)
while Q is not empty:
u = extract_min(Q)
for each vertex v in G.Adj[u]:
if v.distance > u.distance + weight[u][v]:
v.distance = u.distance + weight[u][v]
v.redecessor = u
- Time complexity
- Original algorithm:
- Optimized (Fibonacci-Heap):
Dijkstra 好處是一定能找到最佳解,壞處是當節點變多效率會變很差
Best-First Search (BFS)
BFS 會對每個 point (v) 使用 heuristic function (f(v)) 來預估 v 和終點的最小 cost 路徑,這個 heuristic function 可能是:
- Euclidean Distance
- Manhattan Distance
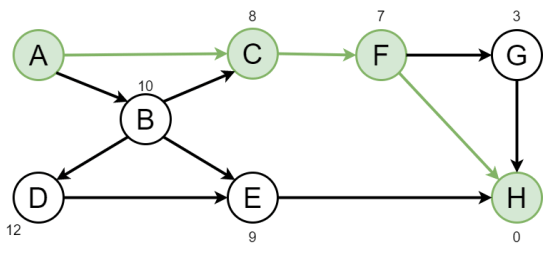
BFS 優點是很快,但缺點是 heuristic 的預測不一定是最佳解
A* Algorithm
A* 則是把 Dijkstra 和 BFS 的優點結合起來,圖中會有兩種參數 (考慮歷史和未來)
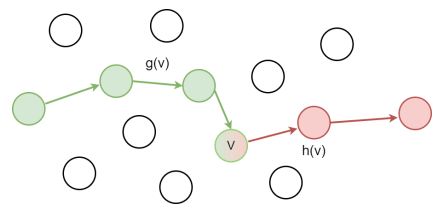
- g(v) 計算從起點到 v 的 cost
- h(v) 計算從 v 到終點的預測 cost
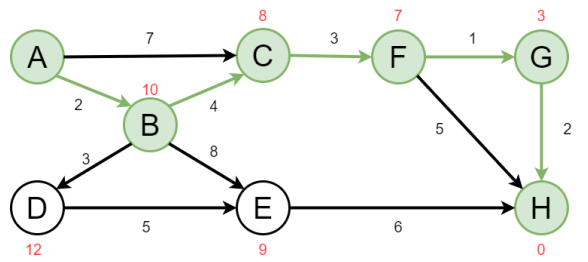
A -> B (2+10) *
-> C (7+8)
B -> C (4+8) *
-> D (3+12)
-> E (8+9)
C -> F (3+7) *
F -> G (1+3) *
-> H (5+0)
G -> H (2+0) *
- 當 h(v) 接近 0 時,則 A* 就會像 Dijkstra 一樣
- 當 g(v) 接近 0 時 (或 h(v) 遠大於 g(v) 時),則 A* 就會像 BFS 一樣
總而言之,決定好的 heuristic function 是最重要的
Heuristic Function
在 mobile robot 中,我們可以將 2D 平面轉化為 grid space,然後就可以依此定義幾種 distance
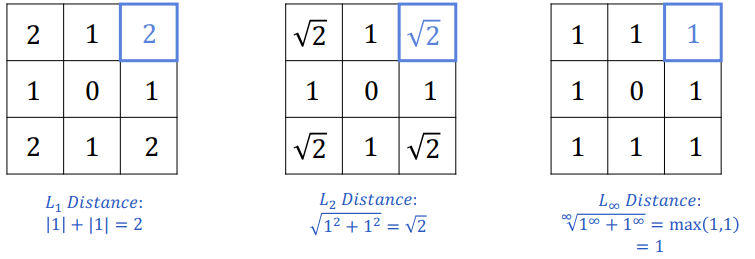
Comparison
- Easy Case

- Hard Case

Sampling Based Planning Methods
因為 A* 依然會搜尋路徑的所有可能 (resolution complete),所以有人提出了 Sampling based planning methods。這個方法利用 sampling 方式來挑選最佳路徑,雖然會找 sub-optimal solution 但能減少搜尋時間 (probabilistic completeness)
PRM
Probabilistic Road-Map (PRM) 是第一種 sampling based planning。PRM 會利用隨機採樣的方式來將 graph 建立成 2D space:
- 從 free area 隨機採樣,移除在 occupied area 的點
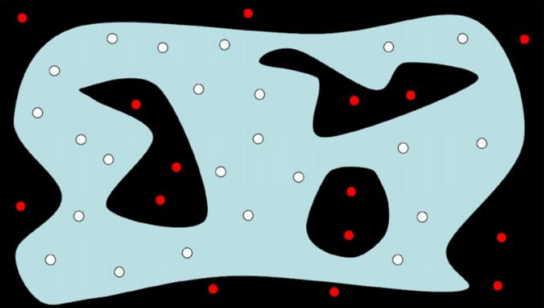
- 連接 k-nearest neighbor points
- 移除穿過 occupied area 的 edges
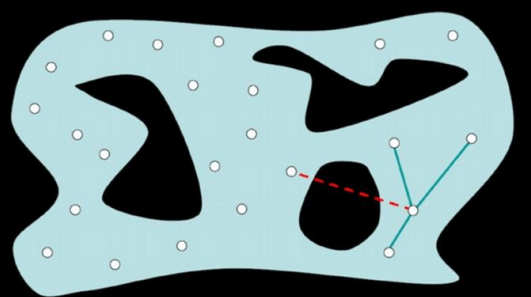
- 連接 connected components
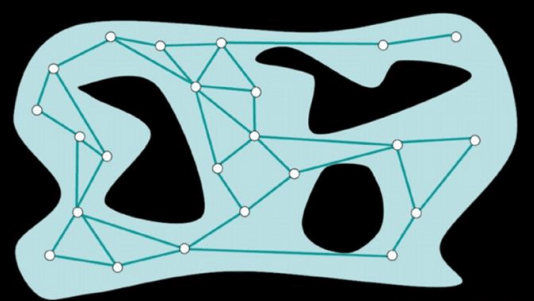
- 就可以從產生的 graph 進行 path planning
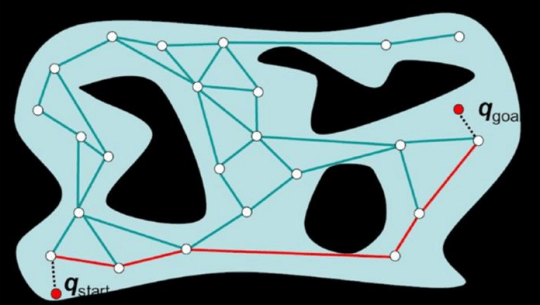
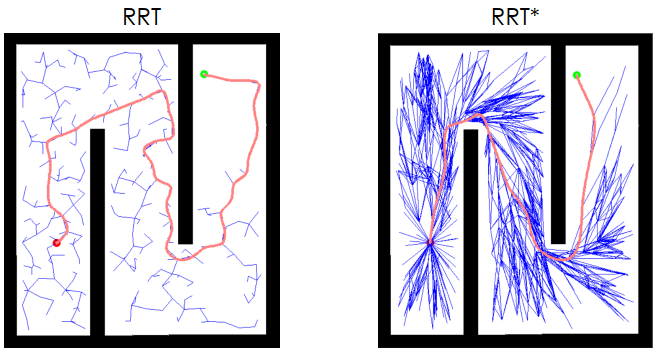
RRT
PRM 建立 graph 還是太慢了,所以又出現了 rapidly exploring random tree (RRT)。RRT 動態建立 tree branch 並且檢查是否有 collision。

挑選隨機點的機率是 P,挑選到終點機率是 (1-P)
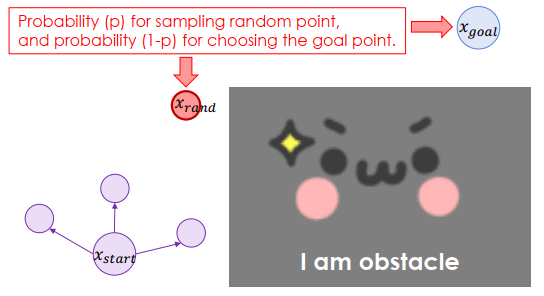
從已建立的 graph 找出離隨機點最近的一點
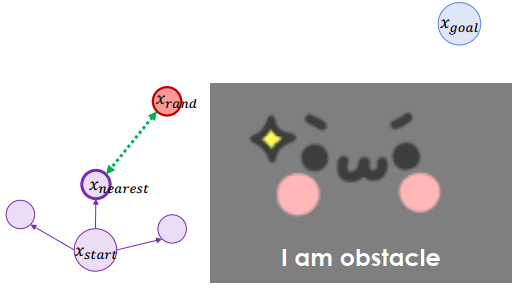
延伸兩者之間的距離
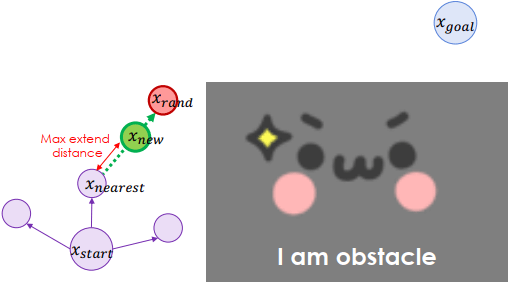
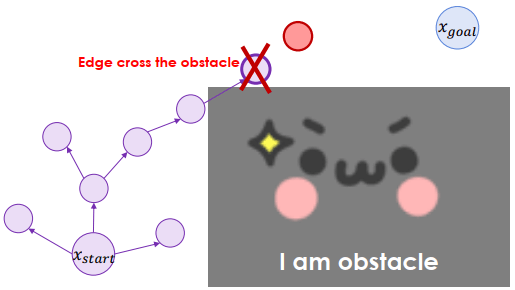
反覆進行一樣的事,但不使用會 cross obstacle 的路徑
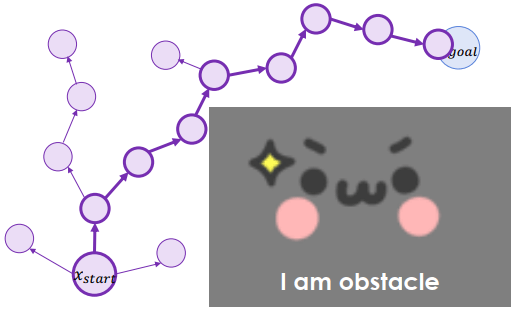
直到要延伸的路徑 < 到終點的路徑,就可以結束了
RRT*
RRT* 是 RRT 的改良版本,現在被廣泛用在 mobile robot 的路徑規劃,他基於 RRT 加入了 re-parent 和 re-wire 的步驟,增加了路徑平滑度。

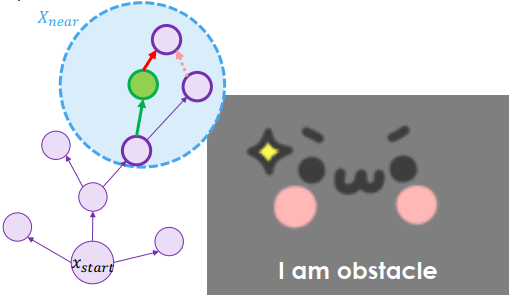
紅色部分是新加入的 re-parent 和 re-wire
Re-parents
從新的節點周圍找出接近的節點,然後計算是否有比原本 parent cost 還要更低的,做為新的 parent
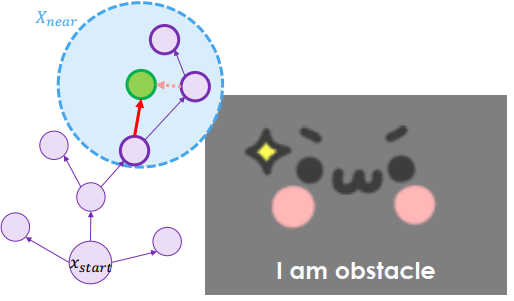
Re-wire
將新節點再做為 parent 連到周圍接近的節點,改變其他節點的 parent (若新節點比他的 parent 的 cost 還要低)
Comparison