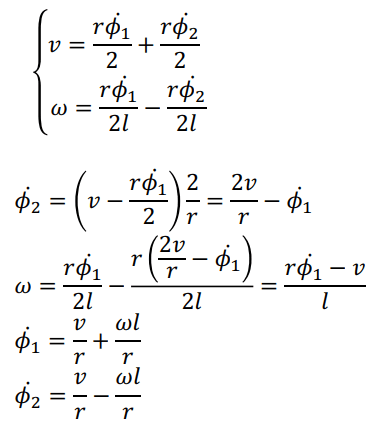Kinetic Model

本文涵蓋了動力學模型以及不同車輛活動模型、Pure Pursuit Control 的原理，以及 bicycle model 的應用。動力學模型用來描述車子的狀態變化，而 Pure Pursuit Control 則是根據速度和角速度來畫圓弧，將車子移動到前方某個點的位置。bicycle model 則是一個根據方向盤轉角來描述車子原點運動的模型。

Basic Kinetic Model

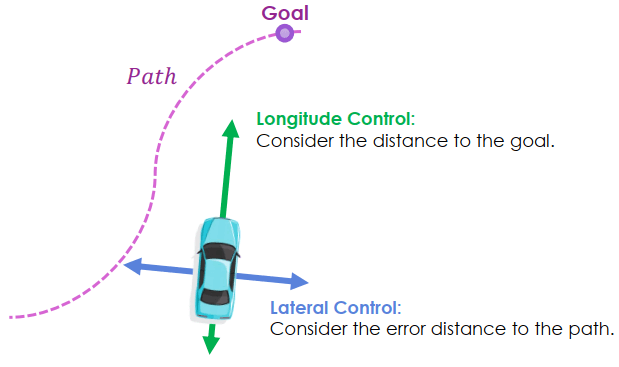
若我們想讓車子移動到路徑上到達終點，可以用前後和左右兩種 control 方式。

Car PID Control

若只使用 PID control 來完成，需要調整太多的參數，所以我們必須要引入一些車輛的特性，來減輕 control system 的負擔：

• 在低速時
  • 可以用簡單的幾何模型來描述 car state
• 在高速時
  • 因會產生側向滑動，所以需要套入更難的動力學模型

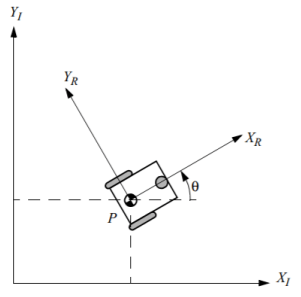
我們用 x, y 代表車子的二維座標，$\theta$ 代表車子的轉向，合起來為車子的狀態

$$\begin{aligned} \text{state: } \xi_1 = \begin{bmatrix}x\\y\\\theta\end{bmatrix} \end{aligned}$$

因為座標有分車子當前的座標，還有世界座標，我們有一個 rotation matrix 可以轉換兩個座標系統

$$\begin{aligned} R(\theta) = \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0& 0& 1 \end{bmatrix} \end{aligned}$$

基本的模型 (basic kinematic model) 指的就是狀態 (state) 的變化 (derivative)

提示

我們會在符號上加上一點代表微分後的變化

Basic Kinematic Model

State 變化可以從車子的當前狀態，乘上 rotation matrix 的反矩陣得到

• $\dot{x_R}$ 是 $x_R$ 的變化，也就是前進速度 ($v$)
• 而側向是沒有速度的，所以 $\dot{y_R} = 0$
• $\dot{\theta}$ 是 $\theta$ 的變化，也就是角速度 ($\omega$)

$$\begin{aligned} \text{Kinematic Model:} \\ \begin{bmatrix}\dot{x} \\ \dot{y} \\ \dot{\theta}\end{bmatrix} &= R(\theta)^{-1}\begin{bmatrix}\dot{x_R}\\\dot{y_R}\\\dot{\theta}\end{bmatrix} \\ &= \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0& 0& 1\end{bmatrix} \begin{bmatrix}v\\0\\\omega\end{bmatrix} \\ &= \begin{bmatrix}v\cos(\theta) \\ v\sin(\theta) \\\omega\end{bmatrix} \end{aligned}$$

Differential Drive Vehicle

Differential Drive Vehicle

現在來考慮兩輪的自走車活動模型

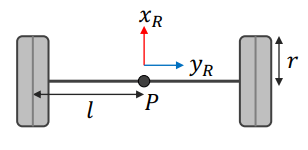
• P: 原點
• l: 原點分別到兩輪的距離
• r: 輪子的半徑
• 座標依然是 $x_R, y_R$

Differential Drive Vehicle

兩輪的轉速分別是 $\phi_1$ 和 $\phi_2$

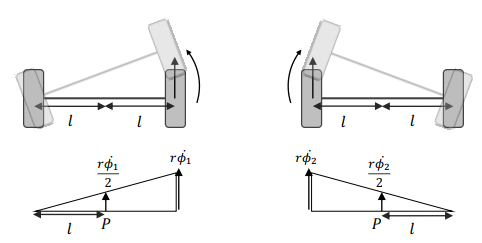
• 右輪 (左輪) 速度 = 半徑 * 角速度
  • $\text{right: } r \times \dot{\phi_1}$
  • $\text{left: } r \times \dot{\phi_2}$
• 原點的速度就是右輪 (左輪) 速度的一半
  • $\dot{x_{R1}} = \frac{r\dot{\phi_1}}{2}$
  • $\dot{x_{R2}} = \frac{r\dot{\phi_2}}{2}$
• 原點的角速度 = 速度 / 到輪子的距離
  • $\omega_1 = \frac{r\dot{\phi_1}}{2l}$
  • $\omega_2 = \frac{-r\dot{\phi_2}}{2l}$
  • 要注意左輪旋轉半徑是 $-l$

而原點的運動就是左右兩輪相加

$$\begin{aligned} \text{Kinematic Model:} \\ \begin{bmatrix}\dot{x} \\ \dot{y} \\ \dot{\theta}\end{bmatrix} &= R(\theta)^{-1}\begin{bmatrix}\dot{x_R}\\\dot{y_R}\\\dot{\theta}\end{bmatrix} \\ &= \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0& 0& 1\end{bmatrix} \begin{bmatrix} \frac{r\dot{\phi_1}}{2}+\frac{r\dot{\phi_2}}{2}\\ 0\\ \frac{r\dot{\phi_1}}{2l}-\frac{r\dot{\phi_2}}{2l} \end{bmatrix} \\ \end{aligned}$$

左右輪的馬達轉速通常不會設成參數，而是用 $v, \omega$ 來推導

RPM Inference

• 直線前進，相同轉速，相同方向 ($\frac{v}{r}$)
• 原地旋轉，相同轉速，相反方向 (正負 $\omega$)

Pure Pursuit Control

Pure pursuit control 將根據速度與角速度來畫圓弧移動到前方某個點的位置

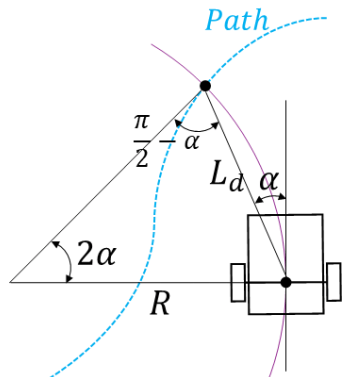
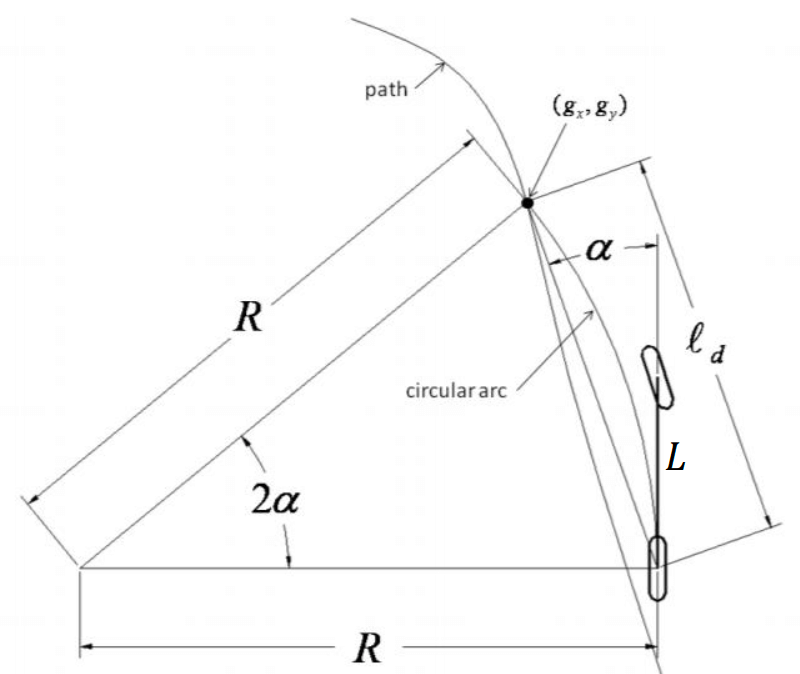
Pure Pursuit Control

• $L_d$ 是車子與目標點的距離
• $R$ 是畫圓產生的半徑
• $\alpha$ 是車子直線方向和 $L_d$ 的夾角
  • $\alpha = \arctan\left(\frac{y-y_g}{x-x_g}\right) - \theta$
  • 因為圓心角 = 兩倍的弦切角
  • 所以圓心角就是 $2 alpha$
• 因為是等腰三角形
  • 所以其他兩個角是 $\frac{\pi}{2} - \alpha$

根據正弦定理可以得到

$$\begin{aligned} \frac{L_d}{\sin(2\alpha)} &= \frac{R}{\sin(\frac{\pi}{2}-\alpha)} \\\\ R &= \frac{L_d\sin(\frac{\pi}{2}-\alpha)}{\sin(2\alpha)} &= \frac{L_d\cos(\alpha)}{2\sin(\alpha)\cos(\alpha)} &= \frac{L_d}{2\sin(\alpha)} \\\\ \omega &= \frac{v}{R} = \frac{2v\sin(\alpha)}{L_d} \end{aligned}$$

也就是說，若速度 v 透過 PID 為已知的值，那就可以推出對應的角速度 ($\omega$)

備註

Ld 通常用速度來決定，速度越快就越遠，例如 $L_d = kv + L_{fc}$，其中的 $k, L_{fc}$ 是可調參數

Kinematic Bicycle Model

上面講的模型可以自由移動旋轉，但真正的車子是有一定的幾何限制 (nonholonomic constraints)。而生活中最常見的移動機構設計是 bicycle model (汽車可以把前後的兩個輪子各別簡化為一個)

• 前輪控制方向 (方向盤)
• 後輪控制速度 (引擎)

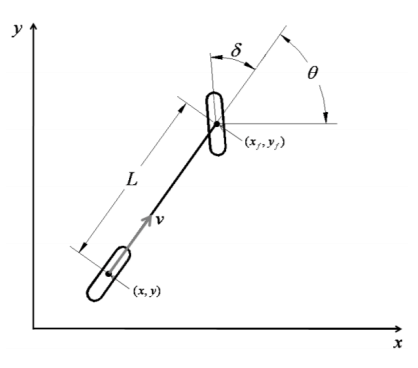
Kinematic Bicycle Model

• 後輪為車輛原點 (x, y)
• 車輛轉向 (車軸方向) $\theta$
• 方向盤轉角 $\delta$
• 車軸長度 $L$

Kinematic Bicycle Model

將前輪放大可以得到一些細節：

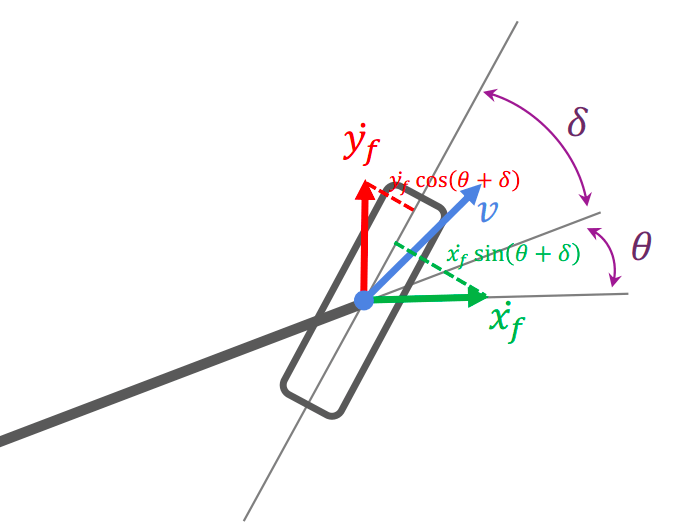
• 車子以 v 的速度向前
• 有兩個世界座標的軸分量 (weight) 為 $\dot{x_f}$ 和 $\dot{y_f}$

計算兩個 weight 對車子垂直方向的 weight

• $\dot{x_f}\sin(\theta+\delta)$
• $\dot{y_f}\cos(\theta+\delta)$

考慮在低速下，兩個 weight 相加會抵消，就可以得到前後輪的 equation (Nonholonomic constraint equations)

$$\begin{aligned} (1) && \dot{x_f}\sin(\theta+\delta) - \dot{y_f}\cos(\theta+\delta) = 0 && \text{(front wheel)}\\ (2) && \dot{x}\sin(\theta) - \dot{y}\cos(\theta) = 0 && \text{(rear wheel)} \end{aligned}$$

我們的目標是算出車輛原點的運動，可以從後輪座標推得前輪座標 (Front wheel position)

$$\begin{aligned} x_f = x + L\cos(\theta) \\ y_f = y + L\sin(\theta) \end{aligned}$$

將前輪座標帶回 (1) 就可以得到基於車輛原點的限制方程式

$$\begin{aligned} (3) && \dot{x}\sin(\theta+\delta) - \dot{y}\cos(\theta+\delta) - \dot{\theta}L\cos(\delta) = 0 \end{aligned}$$

由 (2) 和 (3) 可以得到一組解，代表原點的變化

$$\begin{aligned} (4) && \dot{x} = v\cos(\theta)\\ (5) && \dot{y} = v\sin(\theta) \end{aligned}$$

將 (4) 和 (5) 再帶回 (3) 就可以得到角速度 ($\dot{\theta}$)

$$\dot{\theta} = \frac{v\tan(\delta)}{L}$$

於是我們就可以得到完整的 kinematic bicycle model (基於方向盤轉角 $\delta$)

$$\begin{aligned} \begin{bmatrix} \dot{x}\\\dot{y}\\\dot{\theta} \end{bmatrix} = \begin{bmatrix} \cos(\theta) \\ \sin(\theta) \\ \frac{\tan(\delta)}{L} \end{bmatrix} v \end{aligned}$$

以及一些相關的 properties

$$\begin{aligned} &\bullet R\dot{\theta} = v \\ &\bullet \frac{v\tan(\delta)}{L} = \frac{v}{R} \\ &\bullet \tan(\delta) = \frac{L}{R} \end{aligned}$$

Pure Pursuit Control for Bicycle Model

Bicycle Model Pure Pursuit Control

我們可以將 bicycle model 應用於 pure pursuit control

• $\alpha$ 和 $R$ 和原本的 pure pursuit control 一樣
• 我們可以用上面的 bicycle model properties 來求得方向盤轉角 ($\delta$)

$$\begin{aligned} &\tan(\delta) = \frac{L}{R} \\ &\delta = \arctan\left(\frac{L}{R}\right) = \arctan\left(\frac{2L\sin(\alpha)}{L_d}\right) \end{aligned}$$