本文主要介紹 Stanley Control 和 LQR Control,Stanley Control 是漸進穩定的控制方法,透過計算當前最近目標點的切線、法線做為新的座標系,並利用誤差對時間的變化做為誤差穩定的漸進方法。LQR Control 則是利用 cost function 中的 state 和 control 重要性,並利用 dynamic programming 求得最佳控制。
Pure pursuit control 雖然好用但不夠穩定,而 Stanley control 提供了漸進穩定的效果
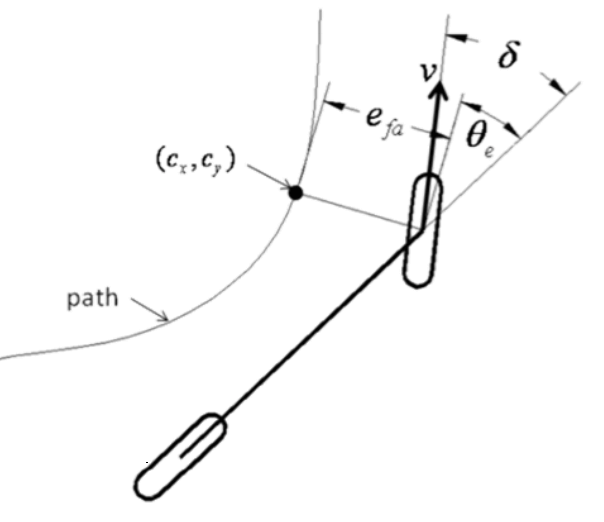
Stanley Control 在 stanley control 會根據當前最近目標點,找到切線、法線 做為新的座標系
v v v δ \delta δ θ e \theta_e θ e δ − θ e \delta - \theta_e δ − θ e 而法線狀態 (微分) 就是以下式子,可以當作追蹤的誤差
e ˙ = v sin ( δ − θ e ) \dot{e} = v\sin(\delta - \theta_e) e ˙ = v sin ( δ − θ e ) 加入誤差對時間變化的假設,希望誤差隨時間變化漸進到 0
e ˙ = − k e , where k > 0 − k e = v sin ( δ − θ e ) δ = arcsin ( − k e v ) + θ e \begin{aligned} \dot{e} &= -ke, \text{ where } k > 0 \\ -ke &= v\sin(\delta - \theta_e) \\ \delta &= \arcsin\left(-\frac{ke}{v}\right) + \theta_e \end{aligned} e ˙ − k e δ = − k e , where k > 0 = v sin ( δ − θ e ) = arcsin ( − v k e ) + θ e 最終可以得到方向盤控制量 δ \delta δ ∣ − k e / v f ∣ > 1 \lvert -ke/vf \rvert > 1 ∣ − k e / v f ∣ > 1
δ = arctan ( − k e v ) + θ e \delta = \arctan\left(-\frac{ke}{v}\right) + \theta_e δ = arctan ( − v k e ) + θ e 改成 arctan 可避免 undefined 但在角度很大時,可能會造成誤差變大
因為太難的運動模型無法直接分析 error function,所以 LQR control 運用 cost function 概念。
運動模型是 linear form Cost function 是 quadratic form cost function c = x T Q x ⏟ state error + u T R u ⏟ minimum control \text{cost function } c = \underbrace{x^TQx}_{\text{state error}} + \underbrace{u^TRu}_{\text{minimum control}} cost function c = state error x T Q x + minimum control u T R u 其中 Q, R 矩陣 分別代表 state, control 在不同維度的重要性,而最終就是要將以下的 total objective function 最小化:
minimize J = ∫ 0 T [ x ( t ) T Q x ( t ) + u ( t ) T R u ( t ) ] d t + x T ( T ) S x ( T ) \text{minimize } J = \int_0^T \left[x(t)^TQx(t) + u(t)^TRu(t)\right]dt + x^T(T) Sx(T) minimize J = ∫ 0 T [ x ( t ) T Q x ( t ) + u ( t ) T R u ( t ) ] d t + x T ( T ) S x ( T ) 若以下狀態從現在到終點 (terminal state) [ u t ∗ , u t + 1 ∗ , u t + 2 ∗ , ⋯ , u T ∗ ] \left[ u_t^\ast ,u_{t+1}^\ast , u_{t+2}^\ast , \cdots , u_T^\ast \right] [ u t ∗ , u t + 1 ∗ , u t + 2 ∗ , ⋯ , u T ∗ ] [ u t + 1 ∗ , u t + 2 ∗ , ⋯ , u T ∗ ] \left[ u_{t+1}^\ast , u_{t+2}^\ast , \cdots , u_T^\ast \right] [ u t + 1 ∗ , u t + 2 ∗ , ⋯ , u T ∗ ] dynamic programming 從最佳解的最終狀態,遞迴解回現在狀態。
通常我們並不知道 terminal state,或者是 terminal state 需要無限時間,這時候我們就會用 value function V ( x ) V(x) V ( x )
V ( x t ) = min u ( x t T Q x t + u t R u t + V ( x t + 1 ) ) V(x_t) = \min_u \left( x_t^TQx_t + u_tRu_t + V(x_{t+1}) \right) V ( x t ) = u min ( x t T Q x t + u t R u t + V ( x t + 1 ) ) V ( x ) V(x) V ( x ) 當前 V = 當下最佳控制的代價 + 下一刻 V 我們可以假設 V ( X ) V(X) V ( X )
V ( x t ) = x t T P t x t V(x_t) = x_t^T P_t x_t V ( x t ) = x t T P t x t 再將 linear motion model (A x t + B u t Ax_t+Bu_t A x t + B u t
V ( x t ) = min u { x t T Q x t + u t R u t + x t + 1 T P t + 1 x t + 1 } = min u { x t T Q x t + u t R u t + ( A x t + B u t ) T P t + 1 ( A x t + B u t ) } = min u { x t T ( Q + A T P t + 1 A ) x t + 2 x T A T P B u + u t T ( R + B T P t + 1 B ) u t } \begin{aligned} V\left(x_{t}\right)& =\min _{\mathbf{u}}\left\{x_{t}^{T} Q x_{t}+u_{t} R u_{t}+x_{t+1}^{T} P_{t+1} x_{t+1}\right\} \\ &=\min _{\mathbf{u}}\left\{x_{t}^{T} Q x_{t}+u_{t} R u_{t}+\left(A x_{t}+B u_{t}\right)^{T} P_{t+1}\left(A x_{t}+B u_{t}\right)\right\} \\ &=\min _{\mathbf{u}}\left\{x_{t}^{T}\left(Q+A^{T} P_{t+1} A\right) x_{t}+2 x^{T} A^{T} P B u+u_{t}^{T}\left(R+B^{T} P_{t+1} B\right) u_{t}\right\} \end{aligned} V ( x t ) = u min { x t T Q x t + u t R u t + x t + 1 T P t + 1 x t + 1 } = u min { x t T Q x t + u t R u t + ( A x t + B u t ) T P t + 1 ( A x t + B u t ) } = u min { x t T ( Q + A T P t + 1 A ) x t + 2 x T A T PB u + u t T ( R + B T P t + 1 B ) u t } 因為我們假設的 value function 是 quadratic 形式,所以可以用微分來求最佳控制 (u ∗ u^\ast u ∗
V ( x t ) = x t T P t x t = min u { x t T ( Q + A T P t + 1 A ) x t + 2 x T A T P B u + u t T ( R + B T P t + 1 B ) u t } ∂ ∂ u [ x t T ( Q + A T P t + 1 A ) x t + 2 x T A T P B u t ∗ + u t ∗ T ( R + B T P t + 1 B ) u t ∗ ] = 0 2 ( x T A T P t + 1 B ) T + 2 ( R + B T P t + 1 B ) u t ∗ = 0 u t ∗ = − ( R + B T P t + 1 B ) − 1 B T P t + 1 A x t \begin{aligned} &V\left(x_{t}\right)=x_{t}^{T} P_{t} x_{t}=\min _{u}\left\{x_{t}^{T}\left(Q+A^{T} P_{t+1} A\right) x_{t}+2 x^{T} A^{T} P B u+u_{t}^{T}\left(R+B^{T} P_{t+1} B\right) u_{t}\right\} \\ &\frac{\partial}{\partial u}\left[x_{t}^{T}\left(Q+A^{T} P_{t+1} A\right) x_{t}+2 x^{T} A^{T} P B u_{t}^{*}+u_{t}^{* T}\left(R+B^{T} P_{t+1} B\right) u_{t}^{*}\right]=0 \\ &2\left(x^{T} A^{T} P_{t+1} B\right)^{T}+2\left(R+B^{T} P_{t+1} B\right) u_{t}^{*}=0 \\ &u_{t}^{*}=-\left(R+B^{T} P_{t+1} B\right)^{-1} B^{T} P_{t+1} A x_{t} \end{aligned} V ( x t ) = x t T P t x t = u min { x t T ( Q + A T P t + 1 A ) x t + 2 x T A T PB u + u t T ( R + B T P t + 1 B ) u t } ∂ u ∂ [ x t T ( Q + A T P t + 1 A ) x t + 2 x T A T PB u t ∗ + u t ∗ T ( R + B T P t + 1 B ) u t ∗ ] = 0 2 ( x T A T P t + 1 B ) T + 2 ( R + B T P t + 1 B ) u t ∗ = 0 u t ∗ = − ( R + B T P t + 1 B ) − 1 B T P t + 1 A x t 得到的 u ∗ u^\ast u ∗ V ( x ) = x t T P t x t V(x) = x_t^TP_tx_t V ( x ) = x t T P t x t
x t T P t x t = x t T ( Q + A T P t + 1 A − A T P t + 1 B ( R + B T P t + 1 B ) − 1 B T P t + 1 A ) x t x_{t}^{T} P_{t} x_{t}=x_{t}^{T}\left(Q+A^{T} P_{t+1} A-A^{T} P_{t+1} B\left(R+B^{T} P_{t+1} B\right)^{-1} B^{T} P_{t+1} A\right) x_{t} x t T P t x t = x t T ( Q + A T P t + 1 A − A T P t + 1 B ( R + B T P t + 1 B ) − 1 B T P t + 1 A ) x t
把兩側的 x x x P P P discrete algebraic Riccati equations (DARE)
P t = Q + A T P t + 1 A − A T P t + 1 B ( R + B T P t + 1 B ) − 1 B T P t + 1 A P_{t}=Q+A^{T} P_{t+1} A-A^{T} P_{t+1} B\left(R+B^{T} P_{t+1} B\right)^{-1} B^{T} P_{t+1} A P t = Q + A T P t + 1 A − A T P t + 1 B ( R + B T P t + 1 B ) − 1 B T P t + 1 A P 代表了前後時刻的轉換方程
順帶一提,在連續的情況下是 continuous algebraic Riccati equations (CARE)
P ˙ = − P A − A T P + P B R − 1 P − Q \dot{P}=-P A-A^{T} P+P B R^{-1} P-Q P ˙ = − P A − A T P + PB R − 1 P − Q 因為 P 不會隨時間變化,所以式子中等式左右的 P 可以改成相同的形式
P = Q + A T P A − A T P t + 1 B ( R + B T P B ) − 1 B T P A P=Q+A^{T} P A-A^{T} P_{t+1} B\left(R+B^{T} P B\right)^{-1} B^{T} P A P = Q + A T P A − A T P t + 1 B ( R + B T PB ) − 1 B T P A 在實作時還可以更簡化,使用 iterative 的方式來求 P 直到收斂
Iteratively find Riccati equation Define: State x = [ e , e ˙ , θ , θ ˙ ] Matrix Q , R \begin{aligned} \text{Define: } \\ &\text{State }x = \left[ e, \dot{e}, \theta, \dot{\theta}\right]\\ &\text{Matrix } Q, R \end{aligned} Define: State x = [ e , e ˙ , θ , θ ˙ ] Matrix Q , R e e e e ˙ \dot{e} e ˙ θ \theta θ θ ˙ \dot{\theta} θ ˙ 兩個改變量存在是為了限制 state 誤差改變量不要太大,接著需要 linear kinematic motion model:
d d t [ e e ˙ θ θ ˙ ] = [ 1 d t 0 0 0 0 v 0 0 0 1 d t 0 0 0 0 ] [ e e ˙ θ θ ˙ ] + [ 0 0 0 v tan ( δ ) L ] \begin{aligned} \frac{d}{d t}\left[\begin{array}{l} e \\ \dot{e} \\ \theta \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{llll} 1 & d t & 0 & 0 \\ 0 & 0 & v & 0 \\ 0 & 0 & 1 & d t \\ 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{l} e \\ \dot{e} \\ \theta \\ \dot{\theta} \end{array}\right]+\left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \frac{v \tan (\delta)}{L} \end{array}\right] \end{aligned} d t d ⎣ ⎡ e e ˙ θ θ ˙ ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 d t 0 0 0 0 v 1 0 0 0 d t 0 ⎦ ⎤ ⎣ ⎡ e e ˙ θ θ ˙ ⎦ ⎤ + ⎣ ⎡ 0 0 0 L v t a n ( δ ) ⎦ ⎤ 橫向距離 = 上個時間點距離 (1) + 橫向速度 (dt) 角度 = 上個時間點角度 (1) + 角速度 (dt) 最後加的方向盤控制量 (δ \delta δ 所以可以用 δ \delta δ tan ( δ ) \tan(\delta) tan ( δ ) ≈ [ 1 d t 0 0 0 0 v 0 0 0 1 d t 0 0 0 0 ] [ e e ˙ θ θ ˙ ] + [ 0 0 0 v L ] δ = A x + B u \begin{aligned} \approx\left[\begin{array}{cccc} 1 & d t & 0 & 0 \\ 0 & 0 & v & 0 \\ 0 & 0 & 1 & d t \\ 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} e \\ \dot{e} \\ \theta \\ \dot{\theta} \end{array}\right]+\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ \frac{v}{L} \end{array}\right] \delta=A x+B u \end{aligned} ≈ ⎣ ⎡ 1 0 0 0 d t 0 0 0 0 v 1 0 0 0 d t 0 ⎦ ⎤ ⎣ ⎡ e e ˙ θ θ ˙ ⎦ ⎤ + ⎣ ⎡ 0 0 0 L v ⎦ ⎤ δ = A x + B u 於是就可以得到 LQR 可解的線性模型 (A x + B u Ax + Bu A x + B u
P = Q + A T P A − A T P B ( R + B T P B ) − 1 B T P A P=Q+A^{T} P A-A^{T} P B\left(R+B^{T} P B\right)^{-1} B^{T} P A P = Q + A T P A − A T PB ( R + B T PB ) − 1 B T P A
再求出最佳的控制量
u t ∗ = − ( R + B T P t + 1 B ) − 1 B T P t + 1 A x t u_{t}^{*}=-\left(R+B^{T} P_{t+1} B\right)^{-1} B^{T} P_{t+1} A x_{t} u t ∗ = − ( R + B T P t + 1 B ) − 1 B T P t + 1 A x t