跳至主要内容

Vehicle Control

本文闡述了控制理論 (Control Theory) 的基本概念，包括開閉環控制 (Open Loop Control, Close Loop Control)、線性時不變系統 (Linear Time Invariant System) 及 PID 控制的概念。

Control Theory​

  • Control system
    • 能夠影響整個系統未來 state 的機制
  • Control theory
    • 因應 output 來改變 input

Open Loop Control​

Open Loop Control
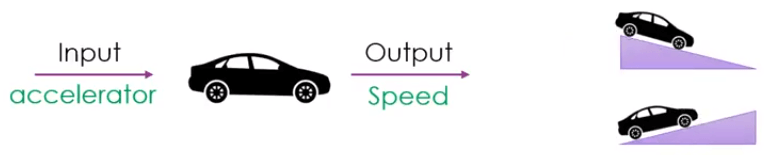
Open Loop Control

例如汽車油門要根據汽車的速度變化 (e.g. 上下坡) 而改變

Open Loop Control Example
Open Loop Control Example

Close Loop Control​

只有 input-output 很難去做修正，所以需要透過前一次 output 來修正

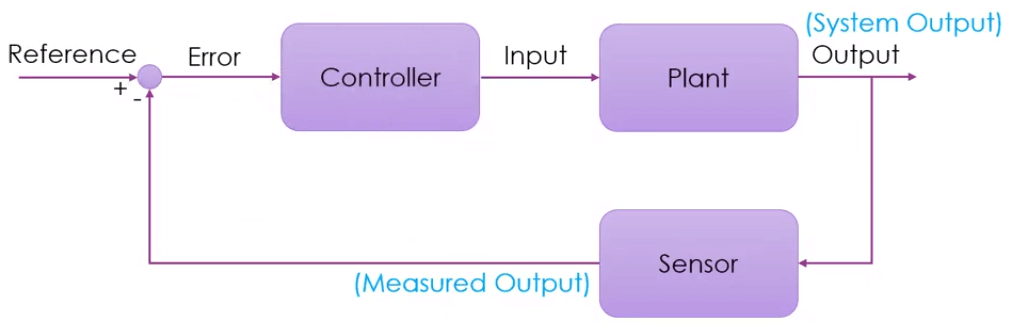
Close Loop Control
Close Loop Control
  • Sensor
    • 量測上一次的 output 結果，用來和 reference 比對
  • Reference
    • 用來比對和 output 的結果，計算出 error
  • Controller
    • 根據 error 改變 input

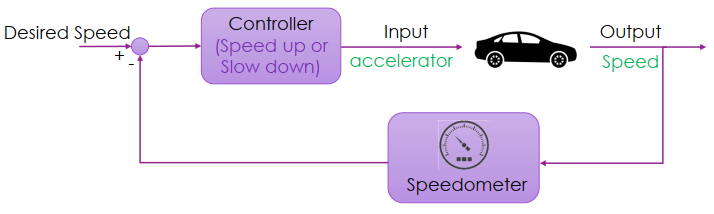
例如根據汽車當前的速度，來調整要加速或減速

Close Loop Control Example
Close Loop Control Example

Linear Time Invariant System​

我們可以將 time domain 轉置成 frequency domain 重整一下 loop control

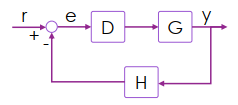
Linear Time Loop Control
Linear Time Loop Control

所有的運算和參數都以頻率來表達

  • G = Input 運算結果
  • H = Sensor 運算結果
  • D = Controller 運算結果
  • r = reference
  • e = error
  • y = output

我們可以得到 e=r−yHe = r - yH (誤差等於 reference 減去 sensor 所算的結果)

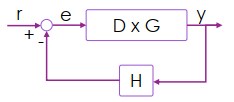
Linear Time Loop Control Combine
Linear Time Loop Control Combine

頻率中 D 到 G 的運算可以視為相乘，我們可以得到 y 等於 e 經過 D 和 G 兩個運算

y=e⋅D⋅Gy = e \cdot D \cdot G

接著經過一連串的運算

e=yDGr−yH=yDG(DG)(r−yH)=yDGr−DGyH=yDGr=y+DGyh=y(1+DGH)y=DGr1+DGH\begin{aligned} e &= \frac{y}{DG} \\ r - yH &= \frac{y}{DG}\\ (DG)(r-yH) &= y\\ DGr -DGyH &= y\\ DGr &= y + DGyh = y(1+DGH)\\ y &= \frac{DGr}{1+DGH} \end{aligned}

於是我們可以將 output (y) 看成是 reference (r) 經過 DG1+DGH\frac{DG}{1+DGH} 運算而來

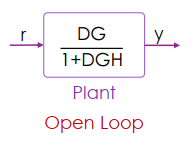
Linear Time Loop Control Open
Linear Time Loop Control Open

變成一個 open loop control

Control Methods​

PID Control​

  • PID 分別為三個詞的縮寫
    • Proportional gain
    • Integral gain
    • Differential gain

Proportional gain​

Controller 設定一個值來與前一個 error 相乘，得到下一次修改的 input，這個值就叫做 proportional gain。 在下圖，老皮根據終點距離來得到 error 並和 0.1 (proportional gain) 相乘：

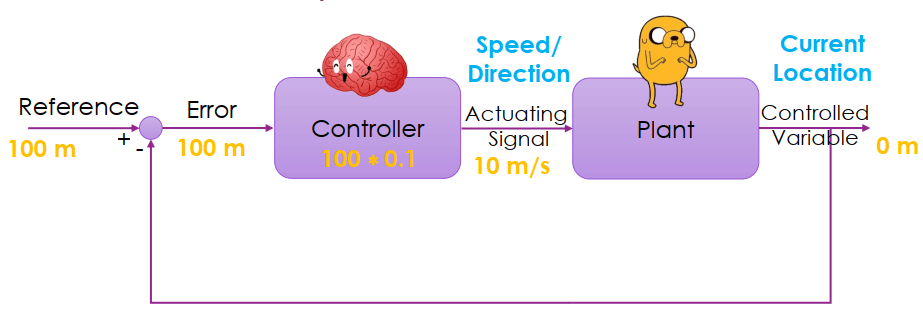
Proportional Gain
Proportional Gain
  • 當距離 100 時，走 10 m/s (100*0.1)
  • 當距離 90 時，走 9 m/s (90*0.1)
  • 當距離 0 時，就停止了 (0*0.1)
Proportional Gain Result
Proportional Gain Result

Problem​

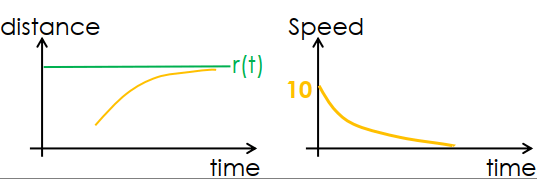
老皮若想往天空飛，那只用 proportional gain 勢必是無法完美達成的，因為最終會停止掉下來，又往上升上去。 假設老皮的螺旋槳轉速 200 rpm 可以對抗重力維持在空中：

Error×Gain=Propeller speed100×2=200rpm40×5=200rpm20×10=200rpm2×100=200rpm\begin{aligned} \text{Error} \times \text{Gain} &= \text{Propeller speed}\\ 100 \times 2 &= 200 \text{rpm}\\ 40 \times 5 &= 200 \text{rpm}\\ 20 \times 10 &= 200 \text{rpm}\\ 2 \times 100 &= 200 \text{rpm}\\ \end{aligned}

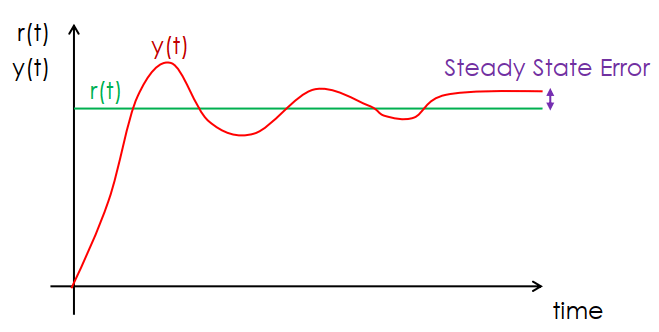
不管設計多少的 gain (2, 5, 10, 100, ...) 都無法讓老皮到達並停留在天空上的終點，這個情況稱為 steady state error (y 會隨時間接近 r，但永遠存在 error)

Steady State Error
Steady State Error

Integral gain​

我們可以加入一個 integrator 來解決 steady state error 造成的問題

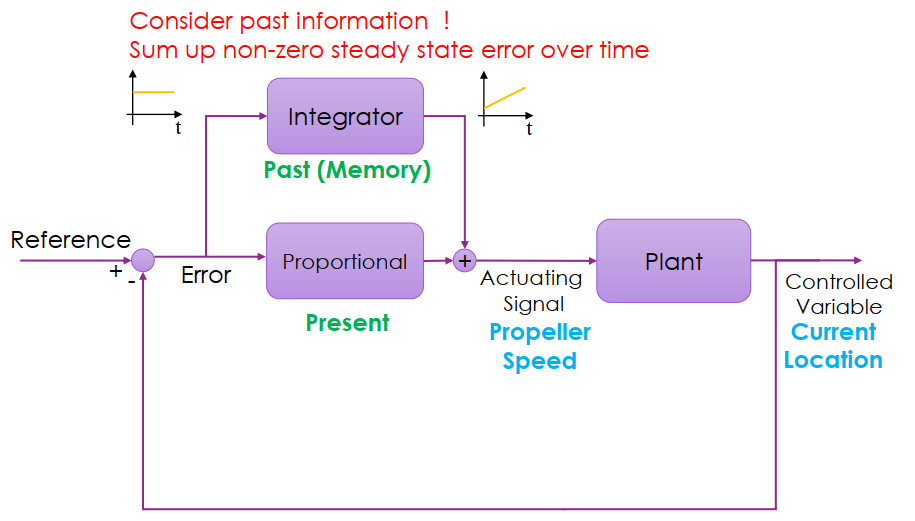
Integral Gain
Integral Gain

新增的 integrator 會累積 error 的資訊來補充 proportional gain 不足的量，例如 error 變成 0 時，integrator 就提供 200 rpm 來讓老皮維持在高空。

Problem​

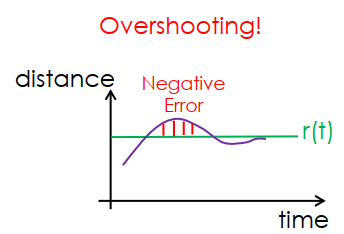
Integrator 若沒有良好設計，會超過 200 rpm 讓老皮繼續往上飛。 而超過 reference 又產生了 negative error，讓 proportional gain 變負，老皮往下降

Integral Gain Problem
Integral Gain Problem

Differential gain​

若能預測 error 變化量，就能預防 integral gain 忽高忽低的問題。

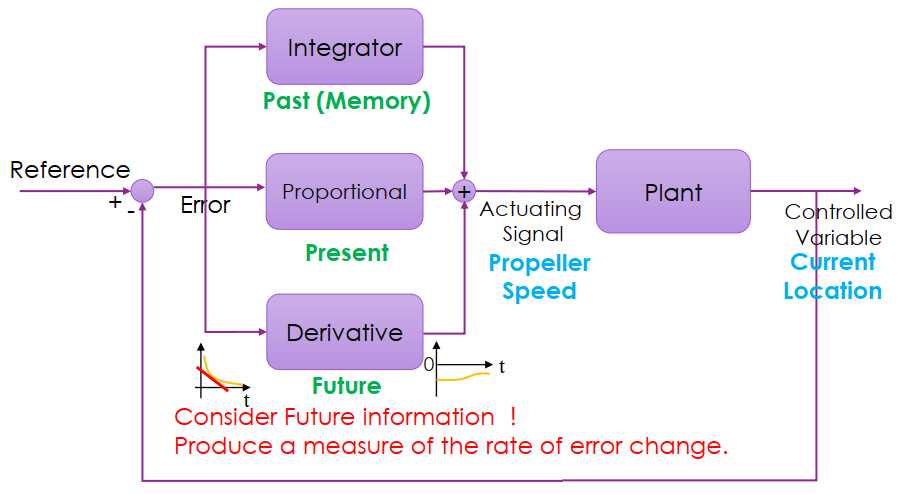
Differential Gain
Differential Gain

我們在 controller 加上第三個 derivative 元件。因為 error 是往下變小的，變化量就是 error 的斜率 (紅線)；因為斜率是負的，所以 derivative 也產生一個負值，來和 integrator 抗衡。

Summary​

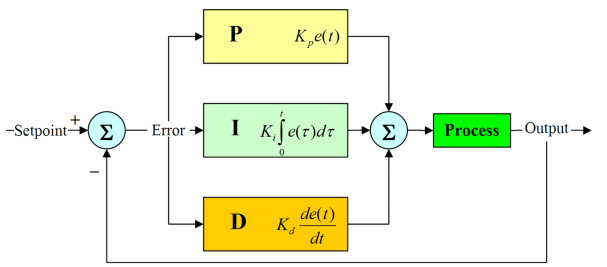
PID Control
PID Control

PID control 可以寫成離散的形式：

Kpe(t)+Ki∑0tet+Kd(e(t)−e(t−1))K_pe(t) + K_i\sum_0^te_t + K_d(e(t)-e(t-1))

其中的 Kp,Ki,KdK_p, K_i, K_d 分別就代表了 proportional, integral, differential gain 的參數。通常就是調整這三個參數，來完成一個好的 controller。